Câu hỏi
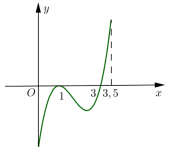
Cho hàm số \(y = f\left( x \right)\) xác định là liên tục trên đoạn \(\left[ {0;\dfrac{7}{2}} \right]\), có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Hỏi hàm số \(y = f\left( x \right)\) đạt GTNN trên đoạn \(\left[ {0;\dfrac{7}{2}} \right]\) tại điểm \({x_0}\) nào dưới đây?
- A \({x_0} = 3\)
- B \({x_0} = 0\)
- C \({x_0} = 1\)
- D \({x_0} = 2\)
Phương pháp giải:
Phương pháp: Hàm số đạt cực trị tại điểm mà tại đó đạo hàm đổi dấu từ âm sang dương (điểm cực tiểu) hoặc từ dương sang âm (điểm cực đại)
Lời giải chi tiết:
Cách giải:
Hàm số đã cho chỉ có điểm \({x_0} = 3\) là đạo hàm đổi dấu (từ âm sang dương) khi đi qua \({x_0}\), do đó \({x_0}\) là điểm cực tiểu và \(f\left( {{x_0}} \right)\) là GTNN của hàm số trên đoạn \(\left[ {0;\dfrac{7}{2}} \right]\).
Chọn đáp án A
Câu hỏi trước
