Câu hỏi
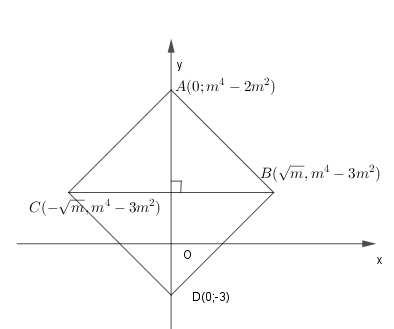
Cho hàm số \(y={{x}^{4}}-2m{{x}^{2}}-2{{m}^{2}}+{{m}^{4}}\) có đồ thị \(\left( C \right).\) Biết đồ thị \(\left( C \right)\) có ba điểm cực trị \(A,B,C\) và \(ABDC\) là hình thoi, trong đó \(D\left( 0;-3 \right),\,A\) thuộc trục tung. Khi đó \(m\) thuộc khoảng nào?
- A \(m\in \left( \frac{9}{5};2 \right).\)
- B \(m\in \left( -1;\frac{1}{2} \right).\)
- C \(m\in \left( 2;3 \right).\)
- D \(m\in \left( \frac{1}{2};\frac{9}{5} \right).\)
Phương pháp giải:
Sử dụng điều kiện cần của cực trị hàm số để tìm điều kiện của \(m\) để hàm số có cực trị. Sau đó tìm tọa độ các điểm cực trị. Sử dụng tính chất của hình thoi để tìm giá trị của \(m.\)
Lời giải chi tiết:
Ta có \(y'=4{{x}^{3}}-4mx.\) Để đồ thị có ba điểm cực trị thì phương trình \(y'=0\Leftrightarrow 4{{x}^{3}}-4mx=0\) phải có \(3\) nghiệm phân biệt.
\(4{{x}^{3}}-4mx=0\Leftrightarrow \left[ \begin{align}& x=0 \\& {{x}^{2}}=m \\\end{align} \right.\)
Khi đó điều kiện cần là \(m>0.\) Ta có ba nghiệm là \(x=0,x=\sqrt{m},x=-\sqrt{m}.\)
Với \(x=0\) thì \(y={{m}^{4}}-2{{m}^{2}}.\)
Với \(x=\pm \sqrt{m}\) thì \(y={{m}^{4}}-3{{m}^{2}}.\)
Do \(A\) thuộc trục tung nên \(A\left( 0;{{m}^{4}}-2{{m}^{2}} \right).\) Giả sử điểm \(B\) nằm bên phải của hệ trục tọa độ, khi đó
\(B\left( \sqrt{m};{{m}^{4}}-3{{m}^{2}} \right),\,\,C\left( -\sqrt{m};{{m}^{4}}-3{{m}^{2}} \right).\)
Ta kiểm tra được \(AD\bot BC.\)
Do đó để \(ABDC\) là hình thoi thì trước hết ta cần
\(\overrightarrow{AB}=\overrightarrow{CD}.\) Ta có
\(\begin{array}{l}\overrightarrow {AB} = \left( {\sqrt m ;\left( {{m^4} - 3{m^2}} \right) - \left( {{m^4} - 2{m^2}} \right)} \right) = \left( {\sqrt m ; - {m^2}} \right),\\\overrightarrow {CD} = \left( {\sqrt m ; - 3 - \left( {{m^4} - 3{m^2}} \right)} \right) = \left( {\sqrt m ; - {m^4} + 3{m^2} - 3} \right).\end{array}\)
Do đó
\(\begin{array}{l}\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left( {\sqrt m ; - {m^2}} \right) = \left( {\sqrt m ; - {m^4} + 3{m^2} - 3} \right) \Leftrightarrow - {m^2} = - {m^4} + 3{m^2} - 3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {m^4} - 4{m^2} + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{m^2} = 1\\{m^2} = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \pm 1\\m = \pm \sqrt 3 \end{array} \right..\end{array}\)
Do điều kiện để có ba điểm cực trị là \(m>0\) nên ta chỉ có \(m=1\) hoặc \(m=\sqrt{3}.\)
Với \(m=1\) thì \(A\left( 0;-1 \right),\,B\left( 1;-2 \right);C\left( -1;-2 \right).\) Ta có \(\overrightarrow{AB}=\left( 1;-1 \right)\Rightarrow AB=\sqrt{2}.\)
Tương tự ta có \(BD=CD=CA=\sqrt{2}.\) Như vậy \(ABDC\) là hình thoi. Vậy \(m=1\) thỏa mãn yêu cầu bài toán.
Do \(m=1\notin \left( \frac{9}{5};2 \right),\left( -1;\frac{1}{2} \right),\left( 2;3 \right)\)nên các đáp án A,B,C đều sai.
Đáp án D đúng.
Với \(m=\sqrt{3}.\) Trong trường hợp này \(B\left( \sqrt[4]{3};0 \right),C\left( -\sqrt[4]{3};0 \right),\,A\left( 0;3 \right).\)Ta kiểm tra được \(AB=BD=DC=CA=\sqrt{9+\sqrt{3}}.\)
Do đó \(ABDC\) cũng là hình thoi và \(m=\sqrt{3}\) thỏa mãn yêu cầu bài toán.
Chọn đáp án D.