Câu hỏi
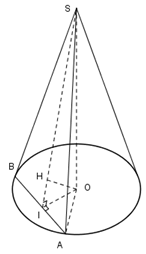
Cho hình nón tròn xoay có chiều cao \(h=20\,cm,\) bán kính đáy \(r=25cm.\) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là \(12cm.\) Tính diện tích của thiết diện đó.
- A \(S=500\left( c{{m}^{2}} \right).\)
- B \(S=400\left( c{{m}^{2}} \right).\)
- C \(S=300\left( c{{m}^{2}} \right).\)
- D \(S=406\left( c{{m}^{2}} \right).\)
Phương pháp giải:
Sử dụng công thức trong tam giác vuông để tính độ dài các cạnh \(IA,SI.\) Sau đó dùng công thức diện tích tam giác để tính diện tích thiết diện.
Lời giải chi tiết:
Tính diện tích của thiết diện \({{S}_{SAB}}.\)
* Diện tích thiết diện: \({{S}_{\Delta SAB}}=\frac{1}{2}AB.SI=\frac{1}{2}\left( 2IA \right).SI=IA.SI\,\,\left( 1 \right).\)
* Xét tam giác vuông \(SOI,\), ta có:\(\frac{1}{H{{O}^{2}}}=\frac{1}{O{{I}^{2}}}+\frac{1}{O{{S}^{2}}}=\frac{1}{{{12}^{2}}}+\frac{1}{{{20}^{^{2}}}}\Rightarrow OH=15\,\left( cm \right).\)
* Mặt khác, xét tam giác vuông \(SOI,\) thì: \(OI.OS=\text{IS}.OH=2{{S}_{\Delta SIO}}\Rightarrow SI=\frac{OS.OI}{OH}=\frac{20.15}{12}=25\,\left( cm \right).\)
* Áp dụng định lý Py-ta-go tam giác vuông \(AIO\) ta có \(IA=\sqrt{O{{A}^{2}}-I{{O}^{2}}}=\sqrt{{{25}^{2}}-{{15}^{2}}}=20\,\left( cm \right)\,\,\left( 3 \right).\)
* Thay \(\left( 2 \right),\,\left( 3 \right)\) vào \(\left( 1 \right)\) ta nhận được \({{S}_{\Delta SAB}}=20.25=500\,\left( c{{m}^{2}} \right).\)
Chọn đáp án A.