Phương pháp giải:

Sử dụng giả thiết ta lập được một hệ phương trình cho bán kính đáy và độ dài đường sinh. Áo dụng định lý Py-ta-go để tìm được độ dài đường cao của nón. Áp dụng công thức thể tích để tìm thể tích của nón.

Lời giải chi tiết:

Gọi \(r,l\) lần lượt là bán kính đáy và độ dài đường sinh của nón.

Khi đó theo công thức diện tích xung quanh ta có \({{S}_{xq}}=\pi .rl.\) Mặt khác \({{S}_{xq}}=6\pi {{a}^{2}}.\)

Do đó \(rl=6{{a}^{2}}\,\,\left( 1 \right).\)

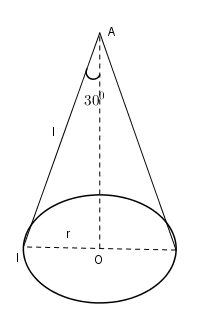
Hạ đường cao \(AO\) xuống đáy. Khi đó theo giả thiết ta có \(\widehat{IAO}={{30}^{0}}.\)

Trong tam giác vuông \(AIO\) ta có \(\sin \widehat{IAO}=\frac{IO}{IA}\Rightarrow \sin {{30}^{0}}=\frac{r}{l}\Rightarrow l=2r\,\,\left( 2 \right).\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có 

\(\left\{ \begin{array}{l}rl = 6{a^2}\\l = 2r\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}r = a\sqrt 3 \\l = 2a\sqrt 3 \end{array} \right..\)

Áp dụng định lý Py-ta-go trong tam giác vuông \(IAO\) ta nhận được \(A{{O}^{2}}=I{{A}^{2}}-I{{O}^{2}}={{l}^{2}}-{{r}^{2}}={{\left( 2a\sqrt{3} \right)}^{2}}-{{\left( a\sqrt{3} \right)}^{2}}=9{{a}^{2}}\Rightarrow AO=3a.\)

Thể tích khối nón là \(V=\frac{1}{3}.AO.{{S}_{\left( O,r \right)}}=\frac{1}{3}.\left( 3a \right).\pi {{r}^{2}}=a.\pi {{\left( a\sqrt{3} \right)}^{2}}=3\pi {{a}^{3}}.\)

Chọn đáp án C.