Câu hỏi
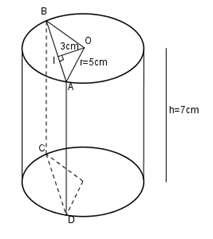
Một hình trụ có bán kính đáy \(r=5\,cm\) và khoảng cách giữa hai đáy \(h=7\,cm.\) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ \(3cm.\) Diện tích của thiết diệt được tạo thành là:
- A \(S=56\,\left( c{{m}^{2}} \right).\)
- B \(S=55\,\left( c{{m}^{2}} \right).\)
- C \(S=53\,\left( c{{m}^{2}} \right).\)
- D \(S=46\,\left( c{{m}^{2}} \right).\)
Phương pháp giải:
Tính độ dài đường cao của hình trụ. Độ dài đường cao này chính là chiều dài của cạnh của thiết diện. Áp dụng công thức tính diện tích hình chữ nhật để tính diện tích thiết diện.
Lời giải chi tiết:
Theo giả thiết ta có \(IO=3\left( cm \right),\,OA=r=5\left( cm \right).\) Giả sử \(ABCD\) là thiết diện cần tìm.
Áp dụng định lý Py-ta-go cho tam giác vuông \(AIO\) ta có \(I{{A}^{2}}=O{{A}^{2}}-I{{O}^{2}}={{5}^{2}}-{{3}^{2}}={{4}^{2}}\Rightarrow IA=4\,\left( cm \right).\)
Theo giả thiết ta có \(AD=h=7\left( cm \right).\)
Từ \(IA=4\left( cm \right)\Rightarrow AB=2IA=2.4=8\left( cm \right).\)
Do đó diện tích thiết diện tạo thành là \({{S}_{ABCD}}=AB.AD=8.7=56\,\left( c{{m}^{2}} \right).\)
Chọn đáp án A.