Câu hỏi
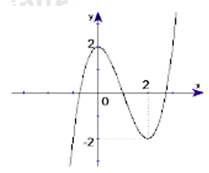
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
- A Hàm số có giá trị cực tiểu bằng 2
- B Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2
- C Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\)
- D Hàm số có ba cực trị.
Phương pháp giải:
Phương pháp. Sử dụng định nghĩa của cực đại, cực tiểu để làm. Cụ thể điểm \({x_0}\) được gọi là điểm cực đại của hàm số \(y = f\left( x \right)\)
nếu trong lân cận V của điểm \({x_0}\) ta có \(f\left( x \right) < f\left( {{x_0}} \right),\,\forall x \in V.\)
Điểm \({x_0}\) được gọi là điểm cực tiểu của hàm số \(y = f\left( x \right)\) nếu trong lân cận V của điểm \({x_0}\) ta có \(f\left( x \right) > f\left( {{x_0}} \right),\,\forall x \in V.\)
Lời giải chi tiết:
Lời giải chi tiết.
Nhìn vào đồ thị ta thấy, hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) nghịch biến trên khoảng \(\left( {0;2} \right).\) Do đó hàm số đã cho đạt cực trị ( địa phương) tại các điểm \(x = 0\) và \(x = 2.\) Hơn nữa trong lân cận của điểm \(x = 0\) thì giá trị của \(y\) lớn nhất là \(2\) do đó hàm số đã cho đạt cực đại tại \(x = 0\) và giá trị cực đại \(y = 2.\) là Tương tự ta có hàm đã cho đạt cực tiểu (địa phương) tại \(x = 2\) và giá trị cực tiểu là \(y = -2.\)
Chọn đáp án C.







