Câu hỏi
Xét các tam giác ABC cân tại A, ngoại tiếp đường tròn có bán kính r = 1. Tìm giác trị nhỏ nhất \({{S}_{\min }}\) của diện tích tam giác ABC?
- A \({{S}_{\min }}=2\pi .\)
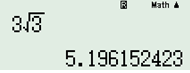
- B \({{S}_{\min }}=3\sqrt{3}.\)
- C \({{S}_{\min }}=3\sqrt{2}.\)
- D \({{S}_{\min }}=4.\)
Lời giải chi tiết:
Phương pháp:
Áp dụng công thức tính diện tích tam giác \(S=p.r\) trong đó p là nửa chu vi và r là bán kính đường tròn nội tiếp tam giác.Cách giải
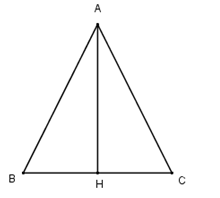
Đặt AB = AC = a, BC = b \(\left( a,b>0 \right)\)
Ta có: \({{S}_{ABC}}=p.r=p.1=p=\frac{a+a+b}{2}=a+\frac{b}{2}\)
Kẻ đường cao AH ta có:
\(\frac{b}{2}=a\sin \frac{A}{2}\Rightarrow {{S}_{ABC}}=a+a\sin \frac{A}{2}\)
Ta lại có
\(\begin{align} & {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\sin A=a+a\sin \frac{A}{2}=a\left( 1+\sin \frac{A}{2} \right) \\ & \Leftrightarrow \frac{1}{2}a\sin A=1+\sin \frac{A}{2} \\ & \Leftrightarrow a=\frac{2\left( 1+\sin \frac{A}{2} \right)}{\sin A} \\ & \Rightarrow {{S}_{ABC}}=\frac{2{{\left( 1+\sin \frac{A}{2} \right)}^{2}}}{\sin A}\,\,\left( 0<A<\pi \right) \\ \end{align}\)
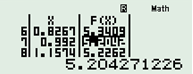
Dùng [MODE] [7] tìm GTNN của hàm số trên ta nhận được:
Xấp xỉ
Chọn B.