Lời giải chi tiết:

Đặt \(\frac{\pi t}{14}=u\Rightarrow u\in \left[ 0;\frac{12\pi }{7} \right)\) khi đó ta có

\(\begin{array}{l}h = 2\sin \left( {3u} \right)\left( {1 - 4{{\sin }^2}u} \right) + 12\\ \Leftrightarrow h = 2\left( {3{\mathop{\rm sinu}\nolimits} - 4{{\sin }^3}u} \right)\left( {1 - 4{{\sin }^2}u} \right) + 12\end{array}\)

Đặt

\(\begin{array}{l}v = \sin u\\ \Rightarrow h\left( v \right) = 2\left( {3t - 4{t^3}} \right)\left( {1 - 4{t^2}} \right) + 12\\ = 6t - 24{t^3} - 8{t^3} + 32{t^5} + 12\\ = 32{t^5} - 32{t^3} + 6t - 12\end{array}\)

Xét \(u \in \left[ {0;\frac{\pi }{2}} \right] \Rightarrow v \in \left[ {0;1} \right]\)

Dùng [MODE] [7] ta có : trong khoảng \(\left( 0,2;0,3 \right)\) có 1 lần hàm số đạt giá trị bằng 13.

trong khoảng \(\left( 0,3;0,4 \right)\) có 1 lần hàm số đạt giá trị bằng 13.

trong khoảng \(\left( 0,9;1 \right)\) có 1 lần hàm số đạt giá trị bằng 13.

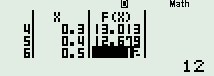
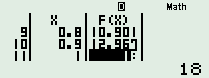
Vậy \(v\in \left[ 0;1 \right]\) thì có 3 lần f(v) = 13.

Xét \(u\in \left[ \frac{\pi }{2};\pi \right]\Rightarrow v\in \left[ 0;1 \right]\). Tương tự như trên ta có 3 lần f(v) = 13.

Xét \(u\in \left[ \pi ;\frac{3\pi }{2} \right]\Rightarrow v\in \left[ -1;0 \right]\) có 2 lần f(v) = 13.

Xét \(u\in \left[ \frac{3\pi }{2};\frac{12\pi }{7} \right)\Rightarrow v\in \left[ -1;\sin \frac{12\pi }{7} \right)\Rightarrow \)có 1 lần f(v) = 13.Vậy có tất cả 9 lần mực nước trong kênh đạt độ sâu 13m.

Chọn D.