Câu hỏi
Tứ giác ABCD có \(\widehat{A\,\,}=110{}^\circ ;\,\,\widehat{B\,\,}=100{}^\circ \) . Các tia phân giác của các góc C và D cắt nhau tại E. Các đương phân giác của các góc ngoài tại đỉnh C và D cắt nhau tại F. Tính \(\widehat{CED};\,\,\,\widehat{CFD}\).
- A \(\widehat{CED}=100^0;\,\,\,\widehat{CFD}=80^0\)
- B \(\widehat{CED}=105^0;\,\,\,\widehat{CFD}=75^0\)
- C \(\widehat{CED}=115^0;\,\,\,\widehat{CFD}=65^0\)
- D \(\widehat{CED}=110^0;\,\,\,\widehat{CFD}=70^0\)
Lời giải chi tiết:
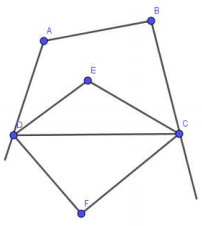
Tứ giác ABCD có:
\(\widehat{C\,\,}+\widehat{D\,\,}=360{}^\circ -\widehat{A\,\,}-\widehat{B\,\,}=360{}^\circ -110{}^\circ -100{}^\circ =150{}^\circ \)
Nên \(\widehat{ECD}+\widehat{EDC}=\left( \widehat{C\,\,}+\widehat{D\,\,} \right):2=150{}^\circ :2=75{}^\circ \)
Xét \(\Delta CED\) có:
\(\widehat{CED}=180{}^\circ -\left( \widehat{ECD}+\widehat{EDC} \right)=180{}^\circ -75{}^\circ =105{}^\circ \)
Vì DE và DF là các tia phân giác của hai góc kề bù nên \(DE\bot DF\) .
Tương tự ta có: \(CE\bot CF\) .
Xét tứ giác CEDF có:
\(\widehat{F\,\,}=360{}^\circ -\widehat{E\,\,}-\widehat{ECF}-\widehat{EDF}=360{}^\circ -105{}^\circ -90{}^\circ -90{}^\circ =75{}^\circ \)







