Câu hỏi
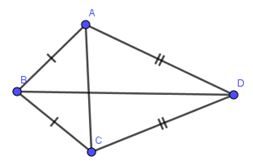
Cho tứ giác ABCD có\(AB=BC,~CD=DA\).
a) Chứng minh rằng BD là đường trung trực của AC.
b) Cho biết \(\widehat{B\,\,}=100{}^\circ ~;\,\,\widehat{D\,\,}=70{}^\circ \) Tính \(\widehat{A\,\,};\,\,\widehat{C\,\,}\) .
- A \(\widehat{BAD}=\widehat{BCD}=100{}^\circ \)
- B \(\widehat{BAD}=\widehat{BCD}=90{}^\circ \)
- C \(\widehat{BAD}=\widehat{BCD}=95{}^\circ \)
- D \(\widehat{BAD}=\widehat{BCD}=105{}^\circ \)
Lời giải chi tiết:
a) Ta có: \(BA=BC(gt);DA=DC(gt)\) nên BD là đường trung trực của AC. (đpcm)
b) Xét \(\Delta ABD\) và \(\Delta CBD\) có:
\(\begin{align}& BA=BC(gt) \\ & DA=DC(gt) \\ \end{align}\)
\(BD\) cạnh chung
Suy ra \(\Delta ABD=\Delta CBD\) (c.c.c)
Suy ra \(\widehat{BAD}=\widehat{BCD}\) ( hai góc tương ứng)
Ta lại có:
\(\widehat{BAD}+\widehat{BCD}=360{}^\circ -\widehat{B\,\,}-\widehat{D\,\,}=360{}^\circ -100{}^\circ -70{}^\circ =190{}^\circ \)
Do đó: \(\widehat{BAD}=\widehat{BCD}=190{}^\circ :2=95{}^\circ \)
Câu hỏi trước
