Phương pháp giải:

a) Tìm vecto \(\overrightarrow {CA} \)

Viết phương trình đường thẳng AC qua A và nhận \(\overrightarrow {CA} \) làm vtcp.

b)

+ Tìm vecto \(\overrightarrow {BC} \)

+ Đường thẳng qua \(M\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n \left( {a;b} \right)\) là vtpt có phương trình:

\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

c)

Đường tròn tâm \(I\left( {{x_0};{y_0}} \right)\) và đi qua M có bán kính R=IM.

Lời giải chi tiết:

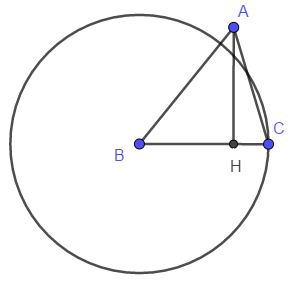
a)

\(\overrightarrow {CA}  = \left( {6; - 5} \right)\)

Đường thẳng AC qua A và nhận \(\overrightarrow {CA}  = \left( {6; - 5} \right)\) làm vtcp có phương trình:

\(\left\{ \begin{array}{l}x = 4 + 6t\\y =  - 3 - 5t\end{array} \right.\left( {t \in \mathbb{R}} \right)\)

b)

\(\overrightarrow {BC}  = \left( { - 4;1} \right)\)

AH là đường thẳng qua A và vuông góc với BC nên nhận vecto \(\overrightarrow {BC} \) làm vtpt:

\(\begin{array}{l} - 4\left( {x - 4} \right) + 1.\left( {y + 3} \right) = 0\\ \Leftrightarrow 4x - y - 19 = 0\end{array}\)

c)

Đường tròn đi qua C nên có bán kính \(R = BC = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {2 - 1} \right)}^2}} \)\( = \sqrt {17} \).

Phương trình của đường tròn cần tìm là:

\({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)