Câu hỏi
Cho điểm A(2;5;1), mặt phẳng \(\left( P \right):6x + 3y - 2z + 24 = 0\). H là hình chiếu vuông góc vủa A trên mặt phẳng (P). Phương trình mặt cầu (S) có diện tích \(784\pi \) và tiếp xúc với mặt phẳng (P) tại H sao cho điểm A nằm trong mặt cầu là:
- A \({\left( {x - 16} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 7} \right)^2} = 196\)
- B \({\left( {x - 8} \right)^2} + {\left( {y - 8} \right)^2} + {\left( {z - 1} \right)^2} = 196\)
- C \({\left( {x - 8} \right)^2} + {\left( {y - 8} \right)^2} + {\left( {z + 1} \right)^2} = 196\)
- D \({\left( {x + 16} \right)^2} + {\left( {y + 4} \right)^2} + {\left( {z - 7} \right)^2} = 196\)
Phương pháp giải:
+ Tìm AH
+ Tìm H.
+ \({S_{mc}} = 4\pi {R^2}\)=> Tìm R.
+ Nhận xét vị trí của I, H, A tìm I.
Lời giải chi tiết:
AH qua \(A\left( {2;5;1} \right)\) và vuông góc với (P) nên có phương trình:
\(\left\{ \begin{array}{l}x = 2 + 6t\\y = 5 + 3t\\z = 1 - 2t\end{array} \right.\left( {t \in \mathbb{R}} \right)\)
Do \(AH \cap \left( P \right) = \left\{ H \right\}\) nên \(H\left( {2 + 6t;5 + 3t;1 - 2t} \right)\). Thay vào (P) ta được:
\(\begin{array}{l}6\left( {2 + 6t} \right) + 3\left( {5 + 3t} \right) - 2\left( {1 - 2t} \right) + 24 = 0\\ \Leftrightarrow t = - 1\\ \Rightarrow H\left( { - 4;2;3} \right)\end{array}\)
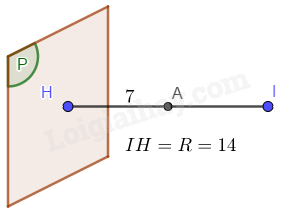
Do mặt cầu tiếp xúc với (P) tại H nên tâm I của mặt cầu thuộc đường thẳng AH và cùng phía với A so với (P).
Diện tích mặt cầu: \(784\pi = 4\pi {R^2} \Rightarrow R = 14 = IH\).
Do I, A, H thẳng hàng, I và A cùng phía so với H và IH=2AH nên A là trung điểm của IH.
\( = > I\left( {8;8; - 1} \right)\).







