Câu hỏi
Cho hàm số \(f\left( x \right) = {x^7} + {x^5} - {x^4} + {x^3} - 2{x^2} + 2x - 10\) và \(g\left( x \right) = {x^3} - 3x + 2\). Đặt \(F\left( x \right) = g\left[ {f\left( x \right)} \right]\). Tìm tất cả các giá trị của tham số \(m\) để phương trình \(F\left( x \right) = m\) có ba nghiệm thực phân biệt
- A \(m \in \left( { - 1;3} \right)\)
- B \(m \in \left( {0;4} \right)\)
- C \(m \in \left( {3;6} \right)\)
- D \(m \in \left( {1;3} \right)\)
Phương pháp giải:
Nhận xét tính chất hàm số \(y = f\left( x \right)\), từ đó suy ra mối tương quan giữa số nghiệm của phương trình với số giá trị của f(x).
Lời giải chi tiết:
Ta có :
\(\begin{array}{l}f'\left( x \right) = 7{x^6} + 5{x^4} - 4{x^3} + 3{x^2} - 4x + 2\\ = 7{x^6} + {x^4} + 4{x^4} - 4{x^3} + {x^2} + 2{x^2} - 4x + 2\\ = 7{x^6} + {x^4} + {x^2}\left( {4{x^2} - 4x + 1} \right) + 2\left( {{x^2} - 2x + 1} \right)\\ = 7{x^6} + {x^4} + {x^2}{\left( {2x - 1} \right)^2} + 2{\left( {x - 1} \right)^2} \ge 0,\forall x \in \mathbb{R}\end{array}\)
Do đó f(x) đồng biến trên R.
Suy ra với mỗi giá trị \(f\left( x \right) = t\) sẽ tồn tại duy nhất một giá trị \({x_0}\) để \(f\left( {{x_0}} \right) = t\)
Xét phương trình \(F\left( x \right) = m \Leftrightarrow g\left( {f\left( x \right)} \right) = m\) (*)
Từ nhận xét trên ta thấy, số nghiệm \(x\) của phương trình (*) bằng số nghiệm \(t\) của phương trình \(g\left( t \right) = m\)
Do đó, để phương trình (*) có 3 nghiệm thực phân biệt thì pt g(t)=m phải có đúng 3 nghiệm t.
Xét hàm \(g\left( t \right) = {t^3} - 3t + 2\) có \(g'\left( t \right) = 3{t^2} - 3 = 3\left( {{t^2} - 1} \right)\)
Cho \(g'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 1\end{array} \right.\)
BBT :
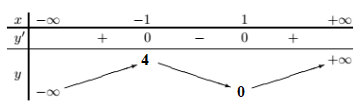
Từ bbt ta thấy, phương trình g(t)=m có đúng 3 nghiệm phân biệt \( \Leftrightarrow 0 < m < 4\).
Chọn B.







