Câu hỏi
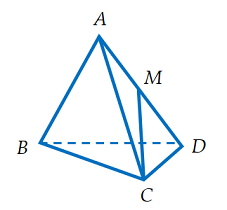
Cho hình tứ diện đều ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh AD (tham khảo hình
vẽ dưới). Tính khoảng cách giữa hai đường thẳng AB và CM theo a
- A \(\dfrac{{a\sqrt {33} }}{{11}}\).
- B \(\dfrac{a}{{\sqrt {33} }}\).
- C \(\dfrac{a}{{\sqrt {22} }}\).
- D \(\dfrac{{a\sqrt {22} }}{{11}}\).
Phương pháp giải:
\(\left\{ \begin{array}{l}a//\left( P \right)\\b \subset \left( P \right)\end{array} \right. \Rightarrow d\left( {a;b} \right) = d\left( {a;\left( P \right)} \right)\)
Lời giải chi tiết:
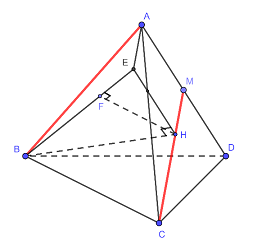
Gọi H là tâm của tam giác đều ACD \( \Rightarrow BH \bot \left( {ACD} \right)\)
Dựng hình chữ nhật AMHE (như hình vẽ). Kẻ HF vuông góc BE.
Do \(CM//AE \subset \left( {ABE} \right) \Rightarrow CM//\left( {ABE} \right) \Rightarrow d\left( {CM;AB} \right) = d\left( {CM;\left( {ABE} \right)} \right) = d\left( {H;\left( {ABE} \right)} \right) = HF\)
Thật vậy:
Ta có: \(\left\{ \begin{array}{l}CM \bot HE\,\,\left( {do\,\,HE//AD} \right)\\CM \bot BH\,\,\left( {do\,\,BH \bot \left( {ACD} \right)} \right)\end{array} \right. \Rightarrow CM \bot \left( {BEH} \right) \Rightarrow CM \bot HF \Rightarrow AE \bot HF\).
Mà \(BE \bot HF \Rightarrow HF \bot \left( {ABE} \right) \Rightarrow d\left( {H;\left( {ABE} \right)} \right) = HF\).
Ta có: \(HE = AM = \dfrac{a}{2}\), \(BH = \sqrt {B{C^2} - C{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
Ta có: \(\dfrac{1}{{H{F^2}}} = \dfrac{1}{{H{E^2}}} + \dfrac{1}{{B{H^2}}} = \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2}}} \Rightarrow HF = \dfrac{{a\sqrt {22} }}{{11}}\)\( \Rightarrow d\left( {CM;AB} \right) = \dfrac{{a\sqrt {22} }}{{11}}\).
Chọn D.







