Câu hỏi
Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng S1 và S2 cách nhau 11cm dao động theo phương vuông góc với mặt nước với cùng phương trình \({u_1} = {u_2} = 5cos\left( {100\pi t} \right)\left( {mm} \right)\). Tốc độ truyền sóng v = 0,5m/s và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1, Ox trùng với S1S2. Trong không gian, phía trên mặt nước có một chất điểm chuyển động mà hình chiếu P của nó tới mặt nước chuyển động với phương trình quỹ đạo \(y = x + 2\) và có tốc độ \({v_1} = 5\sqrt 2 cm/s\). Trong thời gian t = 2s kể từ lúc P có tọa độ xP = 0 thì P cắt bao nhiêu vân cực đại trong vùng giao thoa sóng?
- A 22
- B 14
- C 13
- D 15
Phương pháp giải:
Công thức bước sóng: \(\lambda = v.T = v.\frac{{2\pi }}{\omega }\)
Điều kiện để có cực đại giao thoa là: \({d_1} - {d_2} = k\lambda ;k \in Z\)
Lời giải chi tiết:
Bước sóng:
\(\lambda = v.T = v.\frac{{2\pi }}{\omega } = 50.\frac{{2\pi }}{{100\pi }} = 1cm\)
Trên đoạn nối hai nguồn có số cực đại là số giá trị k thỏa mãn:
\(\begin{array}{l}
- \frac{{{S_1}{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow - \frac{{11}}{1} < k < \frac{{11}}{1} \Rightarrow - 11 < k < 11\\
\Rightarrow k = \pm 10; \pm 9;...0
\end{array}\)
Ta có hình vẽ:
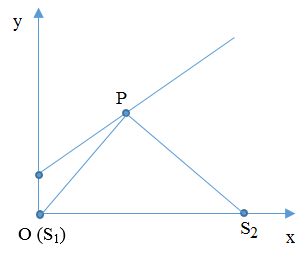
Khi \({x_P} = 0\) , ta có :
\(\left\{ \begin{array}{l}
{S_1}P = 2\\
{S_2}P = \sqrt {{S_1}{S_2}^2 + O{P^2}} = \sqrt {{{11}^2} + {2^2}} = 5\sqrt 5 cm
\end{array} \right.\)
Vậy ta có:
\({S_2}P - {S_1}P = 5\sqrt 5 - 2 = 9,18 = 9,18\lambda \)
Tức là P ban đầu nằm ngoài cực đại bậc 9.
P chuyển động với vận tốc v1, sau thời gian 2 giây thì quãng đường nó đi được là:
\(\begin{array}{l}
S = {v_1}.t = 5\sqrt 2 .2 = 10\sqrt 2 cm\\
\,\,\,\, = \sqrt {{{(x)}^2} + {{(y - 2)}^2}} = \sqrt {{x^2} + {{(x + 2 - 2)}^2}} \\
\Rightarrow x = 10 \Rightarrow y = 12
\end{array}\)
Tọa độ của điểm P lúc đó là (10; 12); tức là x = 10cm; y = 12cm.
Ta có :
\(\left\{ \begin{array}{l}
{S_1}{P_t} = \sqrt {{x^2} + {y^2}} = 2\sqrt {61} cm\\
{S_2}{P_t} = \sqrt {{{(11 - x)}^2} + {y^2}} = \sqrt {145} cm
\end{array} \right.\)
\( \Rightarrow {S_2}{P_t} - {S_1}{P_t} = - 3,57 = - 3,57\lambda \)
Vậy lúc này P nằm ngoài cực đại bậc 3.
Tổng số vân cực đại mà P đã cắt là các vân có:
\(k = 9;8;7; \ldots 0; - 1; - 2; - 3\)
Tổng cộng là 13 vân.
Chọn C.







