Câu hỏi
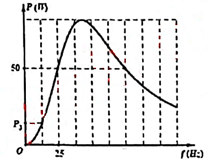
Đặt điện áp \(u = U\sqrt 2 \cos 2\pi ft\) (\(U\) không đổi, \(f\) thay đổi được) vào hai đầu đoạn mạch \(AB\) nối tiếp gồm điện trở \(R\), cuộn cảm thuần \(L\) và tụ điện \(C\). Khi \(f = 25\,\,Hz\) thì \(u\) sớm pha hơn \({u_C}\) là \({60^0}\). Hình vẽ bên là đồ thị phụ thuộc \(f\) của công suất mạch tiêu thụ. Giá trị \({P_3}\) gần giá trị nào nhất sau đây?
- A \(10\,\,{\rm{W}}\).
- B \(9,2\,\,W\).
- C \(6,5\,\,W\).
- D \(18\,\,W\).
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thị
Công suất tiêu thụ: \(P = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Độ lệch pha giữa cường độ dòng điện và hiệu điện thế giữa hai đầu đoạn mạch: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Lời giải chi tiết:
Từ đồ thị ta thấy 2 ô ứng với tần số \(25\,\,Hz\) → 1 ô ứng với tần số \(12,5\,\,Hz\)
Với \({f_1} = 25\,\,Hz\) và \({f_2} = 75\,\,Hz\), công suất tiêu thụ trên mạch có cùng giá trị:
\(\begin{array}{l}{P_1} = {P_2} \Rightarrow \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)}^2}}} = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{{L_2}}} - {Z_{{C_2}}}} \right)}^2}}}\\ \Rightarrow {\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)^2} = {\left( {{Z_{{L_2}}} - {Z_{{C_2}}}} \right)^2}\end{array}\)
Lại có: \({f_2} = 3{f_1} \Rightarrow \left\{ \begin{array}{l}{Z_{{L_2}}} = 3{Z_{{L_1}}}\\{Z_{{C_2}}} = \dfrac{1}{3}{Z_{{C_1}}}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow {\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)^2} = {\left( {3{Z_{{L_1}}} - \dfrac{1}{3}{Z_{{C_1}}}} \right)^2}\\ \Rightarrow \left[ \begin{array}{l}{Z_{{L_1}}} - {Z_{{C_1}}} = 3{Z_{{L_1}}} - \dfrac{1}{3}{Z_{{C_1}}} \Rightarrow - 2{Z_{{L_1}}} = \dfrac{2}{3}{Z_{{C_1}}}\,\,\left( {loai} \right)\\{Z_{{L_1}}} - {Z_{{C_1}}} = - 3{Z_{{L_1}}} + \dfrac{1}{3}{Z_{{C_1}}} \Rightarrow 4{Z_{{L_1}}} = \dfrac{4}{3}{Z_{{C_1}}} \Rightarrow {Z_{{C_1}}} = 3{Z_{{L_1}}} = 3m\,\,\left( {t/m} \right)\end{array} \right.\end{array}\)
Khi tần số \({f_1} = 25\;\,Hz\), độ lệch pha giữa cường độ dòng điện và điện áp giữa hai đầu đoạn mạch là:
\(\begin{array}{l}\varphi = \dfrac{\pi }{2} - \dfrac{\pi }{3} = \dfrac{\pi }{6} \Rightarrow \cos \dfrac{\pi }{6} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {m - 3m} \right)}^2}} }}\\ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{R}{{\sqrt {{R^2} + 4{m^2}} }} \Rightarrow 3{R^2} + 12{m^2} = 4{R^2} \Rightarrow R = 2\sqrt 3 m\end{array}\)
Khi tần số \({f_3} = 12,5\,\,\left( {Hz} \right) = 0,5{f_1} \Rightarrow \left\{ \begin{array}{l}{Z_{{L_3}}} = 0,5{Z_{{L_1}}} = 0,5m\\{Z_{{C_3}}} = 2{Z_{{C_1}}} = 6m\end{array} \right.\), công suất tiêu thụ trên mạch là:
\(\begin{array}{l}\left\{ \begin{array}{l}{P_3} = \dfrac{{{U^2}.2\sqrt 3 m}}{{{{\left( {2\sqrt 3 m} \right)}^2} + {{\left( {0,5m - 6m} \right)}^2}}} = \dfrac{{{U^2}.2\sqrt 3 m}}{{42,25{m^2}}}\\{P_1} = \dfrac{{{U^2}.2\sqrt 3 m}}{{{{\left( {2\sqrt 3 m} \right)}^2} + 4{m^2}}} = \dfrac{{{U^2}.2\sqrt 3 m}}{{16{m^2}}} = 50\end{array} \right.\\ \Rightarrow \dfrac{{{P_3}}}{{{P_1}}} = \dfrac{{16{m^2}}}{{42,25{m^2}}} = \dfrac{{16}}{{42,25}} \Rightarrow {P_3} = \dfrac{{16}}{{42,25}}{P_1} = 18,93\,\,\left( {\rm{W}} \right)\end{array}\)
Chọn D.







