Câu hỏi
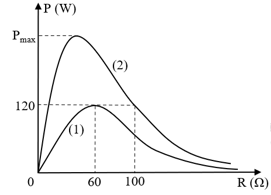
Cho đoạn mạch gồm 3 phần tử R, L, C mắc nối tiếp, trong đó cuộn dây thuần cảm và điện trở R biến thiên. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = {U_0}cos\left( {2\pi ft} \right)\left( V \right)\), \({U_0}\) không đổi nhưng \(f\) có thể thay đổi được. Cho đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ điện của mạch theo R như hình vẽ: Khi \(f = {f_1}\) là đường (1), khi \(f = {f_2}\) là đường (2). Giá trị của \({P_{max}}\) bằng
- A
173W
- B
134W
- C
134W
- D 161W
Phương pháp giải:
+ Đọc đồ thị P-t
+ Sử dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R\)
Lời giải chi tiết:

Ta có:
+ Khi \(f = {f_1}\): \({P_{1max}} = 120W = \dfrac{{{U^2}}}{{2{R_1}}}\) với \({R_1} = 60\Omega \)
Ta suy ra: \(U = 120V\)
+ Khi \(f = {f_2}\):
Tại vị trí \({R_2} = 100\Omega \) có \(P = 120W\)
Ta có: \(P = \dfrac{{{U^2}}}{{R_2^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R_2}\)
\(\begin{array}{l} \Leftrightarrow 120 = \dfrac{{{{120}^2}}}{{{{100}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}.100\\ \Rightarrow \left| {{Z_L} - {Z_C}} \right| = 20\sqrt 5 \Omega \end{array}\)
Lại có: \({P_{2max}} = \dfrac{{{U^2}}}{{2R'}} = \dfrac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \dfrac{{{{120}^2}}}{{2.20\sqrt 5 }} = 72\sqrt 5 W\)
Chọn D







