Câu hỏi
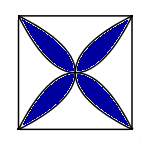
Làng gốm truyền thống Bát Tràng dự kiến làm một bức tranh gồm hình vuông cạnh \(4\,\,\left( m \right)\), thiết kế có 4 đường parabol chung đỉnh tại tâm của hình vuông, tạo nên bốn cánh hoa (tham khảo hình vẽ). Phần diện tích cánh hoa (phần tô đậm) sẽ được tráng một lớp men đặc biệt. Chi phí tráng lớp men đó có đơn giá là 24 triệu đồng/\({m^2}\). Tính số tiền phải trả để tráng men cho 4 cánh hoa.
- A \(132\) triệu
- B \(96\) triệu
- C \(32\) triệu
- D \(128\) triệu
Phương pháp giải:
- Gắn hệ tọa độ vào hình vẽ đã cho.
- Viết phương trình đường parabol tạo thành cánh hoa.
- Áp dụngứng dụng tích phân để tính diện tích hình phẳng để tính diện tích phần tráng men.
Lời giải chi tiết:
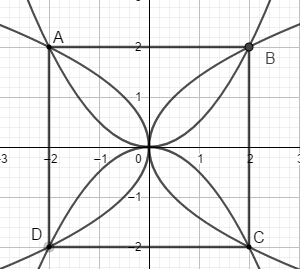
Gắn hệ trục tọa độ như hình vẽ.
Parbol đi qua gốc tọa độ và điểm \(A,\,\,B\) có phương trình \(y = \dfrac{{{x^2}}}{2}\).
Parbol đi qua gốc tọa độ và điểm \(B,\,\,C\) có phương trình \(x = \dfrac{{{y^2}}}{2} \Leftrightarrow {y^2} = 2x \Leftrightarrow y = \sqrt {2x} \,\,\left( {x \ge 0} \right)\).
Diện tích 1 cánh hoa là diện tích hình phẳng giới hạn bởi parabol \(y = \dfrac{{{x^2}}}{2}\);\(y = \sqrt {2x} \), đường thẳng \(x = 2;\,\,x = 0\) là \({S_1} = \int\limits_0^2 {\left( {\sqrt {2x} - \dfrac{{{x^2}}}{2}} \right)dx} = \dfrac{4}{3}\).
\( \Rightarrow \) Diện tích phần tráng men là: \(S = 4{S_1} = \dfrac{16}{3}\,\,\left( {{m^2}} \right)\).
Vậy số tiền cần phải trả là \(T = 24.\dfrac{16}{3} = 128\) triệu.
Chọn D.







