Phương pháp giải:

Sử dụng biểu thức tính tổng hợp dao động: \(x = {x_1} + {x_2} = {A_1}\angle {\varphi _1} + {A_2}\angle {\varphi _2}\)

Lời giải chi tiết:

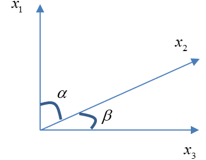
Ta có, trong 1 chu kì: \({x_1}{x_2} < 0\) tại 2 thời điểm đi qua VTCB của \({x_1}\) và \({x_2}{x_3} < 0\) tại 2 thời điểm đi qua VTCB của \({x_2}\)

Ta có: \({t_1} = \dfrac{{2\alpha }}{\omega }\)  và \({t_2} = \dfrac{{2\beta }}{\omega }\)

Lại có: \(\left\{ \begin{array}{l}\alpha  + \beta  = \dfrac{\pi }{2}\\{t_1} = 2{t_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\alpha  = \dfrac{\pi }{3}\\\beta  = \dfrac{\pi }{6}\end{array} \right.\)

Chọn \({\varphi _3} = 0\)

\( \Rightarrow \left\{ \begin{array}{l}{x_3} = 3\angle 0\\{x_2} = 3\angle \dfrac{\pi }{6}\\{x_1} = 3\angle \dfrac{\pi }{2}\end{array} \right.\)

Dao động tổng hợp: \(x = {x_1} + {x_2} + {x_3} = 3\angle \dfrac{\pi }{2} + 3\angle \dfrac{\pi }{6} + 3\angle 0 = 7,18\angle 0,67\) 

\( \Rightarrow \) Biên độ dao động tổng hợp: \(A = 7,18cm\)

Chọn A