Câu hỏi
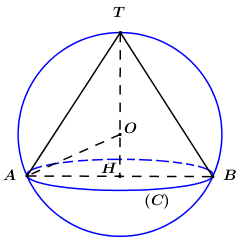
Cho mặt cầu \(\left( S \right)\) tâm \(O\) bán kính \(R = 3\). Mặt phẳng \(\left( P \right)\) cách \(O\) một khoảng bằng 1 và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có tâm là \(H\). Gọi \(T\) là giao điểm của tia \(HO\) và \(\left( S \right)\). Tính thể tích của khối nón đỉnh \(T\) và đáy là hình tròn \(\left( C \right)\).
- A \(\dfrac{{16\pi }}{3}\)
- B \(32\pi \)
- C \(\dfrac{{32\pi }}{3}\)
- D \(16\pi \)
Phương pháp giải:
- Sử dụng định lí Pytago tính bán kính đáy của khối nón.
- Khối nón có chiều cao \(h\), bán kính đáy \(r\) có thể tích là \(V = \dfrac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
Gọi \(AB\) là 1 đường kính của đường tròn \(\left( C \right)\), ta có \(OA = R = 3,\,\,OH = 1\).
Áp dụng định lí Pytago ta có: \(AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{3^2} - {1^2}} = 2\sqrt 2 \).
Do đó khối nón đỉnh \(T\) và có đáy là hình tròn \(\left( C \right)\) có chiều cao \(h = HT - OT + OH = 3 + 1 = 4\), bán kính đáy \(r = AH = 2\sqrt 2 \), do đó thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .{\left( {2\sqrt 2 } \right)^2}.4 = \dfrac{{32\pi }}{3}\).
Chọn C.