Phương pháp giải:

- Tìm ĐKXĐ của hai hàm số.

- Xét phương trình hoành độ giao điểm, cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\), khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\).

- Khảo sát và lập BBT hàm số \(y = f\left( x \right)\), dựa vào BBT tìm giá trị của \(m\) thỏa mãn.

Lời giải chi tiết:

ĐKXĐ: \(x >  - 1,\,\,x \ne 0,\,\,x \ne 1\).

Xét phương trình hoành độ giao điểm \(\dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} = \dfrac{{mx - m - 1}}{{x - 1}}\).

\(\begin{array}{l} \Leftrightarrow \dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} - \dfrac{{mx - m - 1}}{{x - 1}} = 0\\ \Leftrightarrow \dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} = \dfrac{{m\left( {x - 1} \right) - 1}}{{x - 1}}\\ \Leftrightarrow \dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} = m - \dfrac{1}{{x - 1}}\\ \Leftrightarrow \dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} + \dfrac{1}{{x - 1}} = m\end{array}\)

Xét hàm số \(f\left( x \right) = \dfrac{2}{{{5^x}}} + \dfrac{5}{{\ln \left( {x + 1} \right)}} + \dfrac{1}{{x - 1}}\) với \(x >  - 1,\,\,x \ne 0,\,\,x \ne 1\)  ta có:

\(\begin{array}{l}f'\left( x \right) =  - \dfrac{{{{2.5}^x}\ln 5}}{{{5^{2x}}}} - \dfrac{{5.\dfrac{1}{{x + 1}}}}{{{{\ln }^2}\left( {x + 1} \right)}} - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}}\\f'\left( x \right) =  - \dfrac{{2\ln 5}}{{{5^x}}} - \dfrac{5}{{\left( {x + 1} \right){{\ln }^2}\left( {x + 1} \right)}} - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} < 0\,\,\forall x >  - 1,\,\,x \ne 0,\,\,x \ne 1\end{array}\)

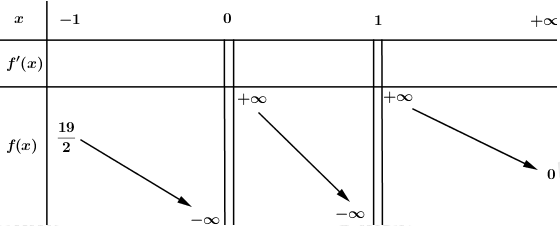
BBT:

Dựa vào BBT ta thấy: Phương trình ban đầu có 3 nghiệm phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt \( \Rightarrow 0 < m < \dfrac{{19}}{2}\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3;4;5;6;7;8;9} \right\}\).

Vậy có \(9\) giá trị của \(m\) thỏa mãn yêu cầu bài toán.

Chọn D.