Câu hỏi
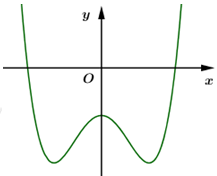
Đường cong trong hình dưới là đồ thị của hàm số \(y = a{x^4} + b{x^2} + c\) với \(a,\,\,b,\,\,c\) là các số thực. Mệnh đề nào dưới đây đúng?
- A Phương trình \(y' = 0\) có ba nghiệm thực phân biệt.
- B Phương trình \(y' = 0\) có hai nghiệm thực phân biệt.
- C Phương trình \(y' = 0\) vô nghiệm trên tập số thực.
- D Phương trình \(y' = 0\) có đúng một nghiệm thực.
Phương pháp giải:
Số nghiệm bội lẻ của phương trình \(y' = 0\) là số cực trị của hàm số \(y = f\left( x \right).\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đã cho có 3 điểm cực trị \( \Rightarrow \) phương trình \(y' = 0\) có 3 nghiệm thực phân biệt.
Chọn A.
Câu hỏi trước
