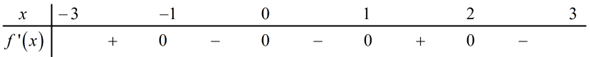Phương pháp giải:

Ta có: \(x = {x_0}\) là điểm cực trị của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số có \(y'\)  đổi dấu từ dương sang âm hoặc ngược lại.

Điểm \(x = {x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số có \(y'\)  đổi dấu từ âm sang dương.

Điểm \(x = {x_0}\) là điểm cực đại của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số có \(y'\)  đổi dấu từ dương sang âm.

Lời giải chi tiết:

Dựa vào BBT ta thấy qua các điểm \(x =  - 1\) và \(x = 2\) thì \(f'\left( x \right)\) đổi dấu từ dương sang âm

\( \Rightarrow x =  - 1\) và \(x = 2\) là các điểm cực đại của hàm số.

Qua điểm \(x = 1\) thì \(f'\left( x \right)\) đổi dấu từ âm sang dương

\( \Rightarrow x = 1\) là điểm cực tiểu của hàm số.

Qua điểm \(x = 0\) thì \(f'\left( x \right)\) không đổi dấu nên \(x = 0\) không là điểm cực trị của hàm số.

Chọn B.