Câu hỏi
Một chất điểm dao động điều hòa có li độ phụ thuộc theo thời gian được biểu diễn như hình vẽ bên. Biết các khoảng chia từ \({t_1}\) trở đi bằng nhau nhưng không bằng khoảng chia từ \(0\) đến \({t_1}\). Quãng đường chất điểm đi được từ thời điểm \({t_2}\) đến thời điểm \({t_3}\) gấp \(2\) lần quãng đường chất điểm đi được từ thời điểm \(0\) đến thời điểm \({t_1}\) và \({t_3} - {t_2} = 0,2\,\,\left( s \right)\). Độ lớn vận tốc của chất điểm tại thời điểm \({t_3}\) xấp xỉ bằng

- A \(42,5\,\,cm/s\).
- B \(31,6\,\,cm/s\).
- C \(27,7\,\,cm/s\).
- D \(16,65\,\,cm/s\).
Phương pháp giải:
Sử dụng vòng tròn lượng giác và kĩ năng đọc đồ thị
Tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
Tốc độ tại li độ x: \({v^2} = {\omega ^2}\left( {{A^2} - {x^2}} \right)\)
Lời giải chi tiết:
Từ đồ thị ta thấy nửa chu kì ứng với 6 ô → 1 chu kì ứng với 12 ô
Khoảng cách mỗi ô là \(0,2\,\,s\)
\( \Rightarrow T = 12.0,2 = 2,4\,\,\left( s \right) \Rightarrow \omega = \dfrac{{2\pi }}{{2,4}} = \dfrac{\pi }{{1,2}}\,\,\left( {rad/s} \right)\)
Với mỗi ô, vecto quay được góc tương ứng là:
\(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{{12}} = \dfrac{\pi }{6}\,\,\left( {rad} \right)\)
Ta có vòng tròn lượng giác:
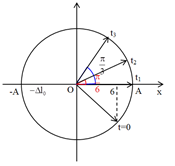
Từ vòng tròn lượng giác, ta thấy quãng đường vật đi từ thời điểm \({t_2}\) đến thời điểm \({t_3}\) là:
\(S = \left| {{x_3} - {x_2}} \right| = \left| {A\cos \dfrac{\pi }{3} - A\cos \dfrac{\pi }{6}} \right| = \dfrac{{A\sqrt 3 }}{2} - \dfrac{A}{2}\)
Theo đề bài ta có:
\(S = 2\left( {A - 6} \right) \Rightarrow \dfrac{{A\sqrt 3 }}{2} - \dfrac{A}{2} = 2.\left( {A - 6} \right) \Rightarrow A = 7,344\,\,\left( {cm} \right)\)
Tốc độ của vật tại thời điểm \({t_3}\) là:
\(\begin{array}{l}{v^2} = {\omega ^2}\left( {{A^2} - {x^2}} \right) = {\omega ^2}.\left( {{A^2} - \dfrac{{{A^2}}}{4}} \right) = {\omega ^2}.\dfrac{3}{4}{A^2}\\ \Rightarrow v = \dfrac{{\sqrt 3 }}{2}\omega A = \dfrac{{\sqrt 3 }}{2}.\dfrac{\pi }{{1,2}}.7,344 = 16,65\,\,\left( {cm/s} \right)\end{array}\)
Chọn D.







