Câu hỏi
Hai điện tích điểm \({q_1} = {2.10^{ - 8}}C;{q_2} = - {3.10^{ - 8}}C\) đặt tại hai điểm A, B trong chân không với \(AB = 30cm.\) Điểm C trong chân không cách A, B lần lượt là \(25cm\) và \(40cm.\) Cho hằng số \(k = 9.10^9\,Nm^2/C^2.\) Cường độ điện trường do hệ hai điện tích gây ra tại C là:
- A \(2568 V/m\)
- B \(4567,5 V/m\)
- C \(4193 V/m\)
- D \(2168,5 V/m\)
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
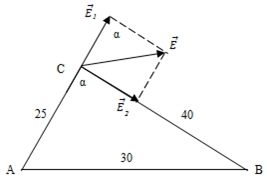
Biểu diễn các vecto cường độ điện trường gây ra tại C trên hình vẽ:
Sử dụng định lí hàm số \(\cos\) trong tam giá ABC có:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.c{\rm{os}}\alpha \\ \Rightarrow c{\rm{os}}\alpha = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = \dfrac{{{{25}^2} + {{40}^2} - {{30}^2}}}{{2.25.30}} = 0,6625\end{array}\)
Cường độ điện trường do q1 và q2 lần lượt gây ra tại C:
\(\left\{ \begin{array}{l}{E_1} = \dfrac{{{{9.10}^9}.\left| {{{2.10}^{ - 8}}} \right|}}{{0,{{25}^2}}} = 2880\left( {V/m} \right)\\{E_2} = \dfrac{{{{9.10}^9}.\left| { - {{3.10}^{ - 8}}} \right|}}{{0,{4^2}}} = 1687,5\left( {V/m} \right)\end{array} \right.\)
Cường độ điện trường do hệ hai điện tích gây ra tại C là:
\(E = \sqrt {E_1^2 + E_2^2 - 2{E_1}{E_2}.c{\rm{os}}\alpha } \)
\( \Rightarrow E = \sqrt {{{2880}^2} + 1687,{5^2} - 2.2880.1687,5.0,6625} = 2168,5(V/m)\)
Chọn D.