Lời giải chi tiết:

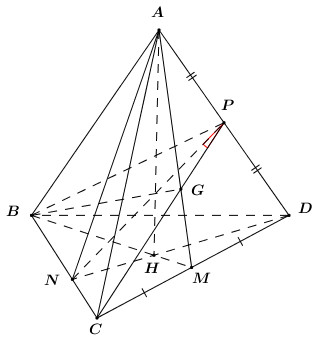
Gọi \(BM,\,\,DN\) lần lượt là các đường cao của tam giác \(BCD\) \( \Rightarrow BM \cap DN = \left\{ H \right\}\).

Ta có: \(\left\{ \begin{array}{l}CD \bot BM\\CD \bot AH\end{array} \right. \Rightarrow CD \bot \left( {ABM} \right) \Rightarrow CD \bot AM\).

\( \Rightarrow AM\) là đường cao của tam giác đều \(ACD\), do đó \(M\) là trung điểm của \(CD\).

Gọi \(P\) là trung điểm của \(AD\), do \(\Delta ACD\) đều nên \(CP \bot AD\).

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AH\\BC \bot DN\end{array} \right. \Rightarrow BC \bot \left( {ADN} \right) \Rightarrow BC \bot AD\\\left\{ \begin{array}{l}AD \bot BC\\AD \bot CP\end{array} \right. \Rightarrow AD \bot \left( {BCP} \right) \Rightarrow AD \bot NP\end{array}\)

Ta có: \(\left\{ \begin{array}{l}\left( {ADN} \right) \cap \left( {ACD} \right) = AD\\NP \subset \left( {ADN} \right),\,\,NP \bot AD\,\,\left( {cmt} \right)\\CP \subset \left( {ACD} \right),\,\,CP \bot AD\,\,\left( {cmt} \right)\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ADN} \right);\left( {ACD} \right)} \right) = \angle \left( {NP;CP} \right) = \angle NPC = {45^0}\).

Ta có: \(BC \bot \left( {ADN} \right)\,\,\left( {cmt} \right) \Rightarrow CN \bot NP\) \( \Rightarrow NCP\) vuông tại \(N\), lại có \(\angle NPC = {45^0}\,\,\left( {cmt} \right)\) \( \Rightarrow \angle NCP = {45^0}\) hay \(\angle BCP = {45^0}\)  (1).

Gọi \(G = AM \cap CP \Rightarrow G\) là trọng tâm tam giác đều \(ACD\).

Ta có:

\(\left\{ \begin{array}{l}AD \bot \left( {BCP} \right)\,\,\left( {cmt} \right) \Rightarrow AD \bot BG\\CD \bot \left( {ABM} \right)\,\,\left( {cmt} \right) \Rightarrow CD \bot BG\end{array} \right.\) \( \Rightarrow BG \bot \left( {ACD} \right)\), mà \(G\) là trọng tâm tam giác đều \(ACD\) \( \Rightarrow BA = BC = BD = a\sqrt 6 \).

Ta có \(BG \bot \left( {ACD} \right) \Rightarrow BG \bot CG\) \( \Rightarrow \Delta BCG\) vuông tại \(G\)  (2).

Từ (1) và (2) suy ra tam giác \(BCG\) vuông cân tại \(G\) \( \Rightarrow BG = CG = \dfrac{{BC}}{{\sqrt 2 }} = a\sqrt 3 \).

Ta có: \(CP = \dfrac{3}{2}CG = \dfrac{{3a\sqrt 3 }}{2} = AC\dfrac{{\sqrt 3 }}{2}\)   đều cạnh \(3a\) nên \({S_{\Delta ACD}} = \dfrac{{{{\left( {3a} \right)}^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\).

Vậy \({V_{ABCD}} = \dfrac{1}{3}BG.{S_{\Delta ACD}} = \dfrac{1}{3}.a\sqrt 3 .\dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{9{a^3}}}{4}\).

Chọn C.