Câu hỏi
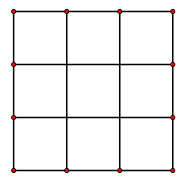
Cho một bảng gồm 9 ô vuông đơn vị như hình vẽ bên. Một em bé cầm 4 hạt đậu đặt ngẫu nhiên vào 4 ô vuông đơn vị trong bảng. Xác suất để bất kì hàng nào và cột nào của bảng cũng có hạt đậu bằng:
- A \(\dfrac{3}{7}\)
- B \(\dfrac{2}{7}\)
- C \(\dfrac{3}{{14}}\)
- D \(\dfrac{5}{{14}}\)
Lời giải chi tiết:
Không gian mẫu: \(n\left( \Omega \right) = C_9^4 = 126\).
Gọi A là biến cố: “bất kì hàng nào và cột nào của bảng cũng có hạt đậu”, khi đó ta có biến cố đối: \(\overline A \): “có 1 hàng hoặc 1 cột không có hạt đậu”.
Gọi B là biến cố: 1 hàng không có đậu.
- Chọn 1 hàng trong 3 hàng có \(C_3^1\) cách.
- Xếp 4 hạt đậu vào 2 hàng còn lại có \(C_6^4\) cách.
\( \Rightarrow \) \(n\left( B \right) = C_3^1.C_6^4 = 45\) cách.
Gọi C là biến cố: 1 cột không có đậu.
- Chọn 1 cột trong 3 cột có \(C_3^1\) cách.
- Xếp 4 hạt đậu vào 2 cột còn lại có \(C_6^4\) cách.
\( \Rightarrow \) \(n\left( C \right) = C_3^1.C_6^4 = 45\) cách.
Ta có: \(B \cap C\) = “1 hàng không có đậu và 1 cột không có đậu”.
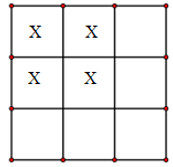
- Chọn 1 hàng không có đậu có \(C_3^1\) cách.
- Chọn 1 cột không có đậu có \(C_3^1\) cách.
- Xếp 4 hạt đậu vào 4 ô còn lại có 1 cách.
\( \Rightarrow n\left( {B \cap C} \right) = 9\).
\( \Rightarrow n\left( A \right) = n\left( B \right) + n\left( C \right) - n\left( {B \cap C} \right) = 45 + 45 - 9 = 81\).
Vậy \(P\left( A \right) = 1 - P\left( {\bar A} \right) = 1 - \dfrac{{81}}{{126}} = \dfrac{5}{{14}}\).
Chọn D.







