Phương pháp giải:

- Cô lập \(m\), đưa phương trình đã cho về dạng \(f\left( x \right) = m\).

- Khảo sát, lập BBT và kết luận giá trị của \(m\) để phương trình có nghiệm.

Lời giải chi tiết:

Ta có: \({6^x} + {4^x} + m{.2^x} = 0\)\( \Leftrightarrow m = \dfrac{{{6^x} + {4^x}}}{{ - {2^x}}} =  - {3^x} - {2^x}\,\,\,\left( * \right)\).

Đặt \(f\left( x \right) =  - {3^x} - {2^x}\), khi đó ta có \(m = f\left( x \right)\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\).

Xét hàm số \(f\left( x \right) =  - {3^x} - {2^x}\) có TXĐ \(D = \mathbb{R}\).

Ta có \(f'\left( x \right) =  - {3^x}\ln 3 - {2^x}\ln 2 < 0\,\,\forall x \in \mathbb{R}\), do đó hàm số nghịch biến trên \(\mathbb{R}\).

\(\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = 0,\,\,\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  - \infty \).

BBT:

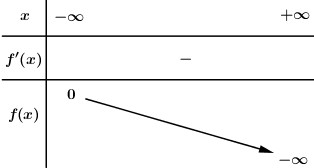
Dựa vào BBT ta thấy để phương trình (*) có nghiệm thì \(m < 0\).

Vậy \(m \in \left( { - \infty ;0} \right)\).

Chọn C.