Câu hỏi
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau:
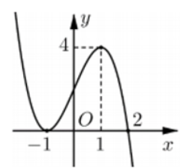
Khẳng định nào sau đây là đúng?
- A Hàm số đạt cực tiểu tại \(x = - 1.\)
- B Hàm số không có điểm cực trị.
- C Hàm số đạt cực đại tại \(x = 4.\)
- D Giá trị cực tiểu của hàm số bằng \( - 1.\)
Phương pháp giải:
Dựa vào đồ thị hàm số, nhận xét các điểm cực đại, cực tiểu của hàm số. Từ đó chọn đáp án đúng.
+) \(x = {x_0}\) là điểm cực tiểu của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số đang tăng sau đó giảm.
+) \(x = {x_0}\) là điểm cực đại của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số đang giảm sau đó tăng.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy hàm số có điểm cực tiểu là \(x = - 1\) và giá trị cực tiểu là \({y_{CT}} = 0.\)
Hàm số có điểm cực đại là \(x = 1\) và giá trị cực đại là \({y_{CD}} = 4.\)
\( \Rightarrow \) Chỉ có đáp án A đúng.
Chọn A.







