Câu hỏi
Cho hình chóp \(S.ABC\) có tam giác \(ABC\) vuông cân tại \(C\), tam giác \(SAB\) vuông tại \(A\), tam giác \(SAC\) cân tại \(S\). Biết \(AB = 2a\), đường thẳng \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) góc \({45^0}\). Thể tích khối chóp \(S.ABC\) bằng:
- A \(\dfrac{{{a^3}\sqrt {10} }}{2}\)
- B \(\dfrac{{{a^3}\sqrt {10} }}{6}\)
- C \({a^3}\sqrt 5 \)
- D \(\dfrac{{{a^3}\sqrt 5 }}{3}\)
Phương pháp giải:
Đặt hệ trục tọa độ.
Lời giải chi tiết:
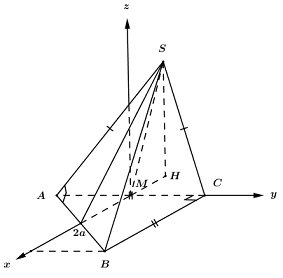
Gọi \(M\) là trung điểm của \(AC\), \(N\) là trung điểm của \(AB\) ta có:
\(\left\{ \begin{array}{l}AC \bot SM\\AC \bot MN\,\,\left( {MN\parallel AB} \right)\end{array} \right. \Rightarrow AC \bot \left( {SMN} \right)\).
Trong \(\left( {SMN} \right)\) kẻ \(SH \bot MN\,\,\left( {H \in MN} \right)\), khi đó ta có: \(\left\{ \begin{array}{l}SH \bot MN\\SH \bot AC\end{array} \right. \Rightarrow SH \bot \left( {ABC} \right)\).
Đặt hệ trục tọa độ như hình vẽ, coi \(a = 1\) ta có: \(M\left( {0;0;0} \right)\).
Tam giác \(ABC\) vuông cân tại \(C\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = a\sqrt 2 \) \( \Rightarrow AM = MC = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow A\left( {0; - \dfrac{{\sqrt 2 }}{2};0} \right),\,\,C\left( {0;\dfrac{{\sqrt 2 }}{2};0} \right)\), \(B\left( {\sqrt 2 ;\dfrac{{\sqrt 2 }}{2};0} \right)\).
TH1: Đặt \(SH = x,\,\,HM = y\,\,\left( {x,\,\,y > 0} \right)\), khi đó ta có \(S\left( {y;0;x} \right)\), \(H\left( {y;0;0} \right)\).
Ta có: \(\overrightarrow {SA} = \left( { - y; - \dfrac{{\sqrt 2 }}{2}; - x} \right),\,\,\overrightarrow {AB} = \left( {\sqrt 2 ;\sqrt 2 ;0} \right)\).
Tam giác \(SAB\) vuông tại \(A\) \( \Rightarrow \overrightarrow {SA} .\overrightarrow {AB} = 0\).
\( \Leftrightarrow - \sqrt 2 y - 1 = 0 \Leftrightarrow y = - \dfrac{1}{{\sqrt 2 }}\) (Vô lí), chứng tỏ điểm \(H\) nằm ngoài đoạn thẳng \(MN\) về phía điểm \(M\).
TH2: Khi đó ta có \(HM = - y\,\,\left( {y > 0} \right)\) \( \Rightarrow S\left( { - y;0;x} \right),\,\,H\left( { - y;0;0} \right)\).
Ta có: \(\overrightarrow {SA} = \left( {y; - \dfrac{{\sqrt 2 }}{2}; - x} \right),\,\,\overrightarrow {AB} = \left( {\sqrt 2 ;\sqrt 2 ;0} \right)\).
Tam giác \(SAB\) vuông tại \(A\) \( \Rightarrow \overrightarrow {SA} .\overrightarrow {AB} = 0\) \( \Leftrightarrow \sqrt 2 y - 1 = 0 \Leftrightarrow y = \dfrac{1}{{\sqrt 2 }}\).
Ta có \(SH \bot \left( {ABC} \right)\) nên \(HB\) là hình chiếu của \(SB\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;HB} \right) = \angle SBH = {45^0}\).
\( \Rightarrow \Delta SBH\) vuông cân tại \(H\) \( \Rightarrow SH = HB\)
\(\begin{array}{l} \Rightarrow {x^2} = {\left( {y + \sqrt 2 } \right)^2} + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} + {0^2}\\ \Leftrightarrow {x^2} = {\left( {\dfrac{1}{{\sqrt 2 }} + \sqrt 2 } \right)^2} + \dfrac{1}{2} = 5 \Leftrightarrow x = \sqrt 5 \\ \Rightarrow SH = a\sqrt 5 \end{array}\)
\({S_{ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.{\left( {a\sqrt 2 } \right)^2} = {a^2}\).
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.a\sqrt 5 .{a^2} = \dfrac{{{a^3}\sqrt 5 }}{3}\).
Chọn D.







