Phương pháp giải:

- Tính bán kính ngoại tiếp đáy hình chóp chính là bán kính đáy hình nón.

- Xác định góc giữa mặt bên và mặt đáy là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính chiều cao hình chóp chính là chiều cao hình nón. Sử dụng định lí Pytago trong tam giác vuông.

- Áp dụng công thức tính diện tích xung quanh khối nón có đường sinh \(l\), bán kính đáy \(R\) là \({S_{xq}} = \pi Rl\).

Lời giải chi tiết:

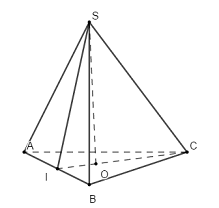
Gọi O là tâm tam giác đều  ABC\( \Rightarrow SO \bot \left( {ABCD} \right)\)

Tam giác ABC đều cạnh a  nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OC = \dfrac{2}{3}CI = \dfrac{{a\sqrt 3 }}{3}\) và \(OI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\).

\( \Rightarrow \) Bán kính khối nón đỉnh \(S\) có đáy là hình tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3}\).

Gọi I là trung điểm của AB ta có: \(\left\{ \begin{array}{l}AB \bot OI\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot SI\).

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\SI \subset \left( {SAB} \right);\,\,SI \bot AB\\CI \subset \left( {ABC} \right);\,\,CI \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABC} \right)} \right) = \angle \left( {SI;CI} \right) = \angle SIC = {60^0}\).

Xét tam giác vuông \(SOI\) có: \(SI = \dfrac{{OI}}{{\cos {{60}^0}}} = \dfrac{{a\sqrt 3 }}{3}\).

Áp dụng định lí Pytago trong tam giác vuông \(SAI\) có: \(SA = \sqrt {S{I^2} + A{I^2}}  = \sqrt {\dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt {21} }}{6}\).

\( \Rightarrow \) Độ dài đường sinh của khối nón đỉnh \(S\) có đáy là hình tròn ngoại tiếp tam giác \(ABC\) là \(l = \dfrac{{a\sqrt {21} }}{6}\).

Vậy diện tích xung quanh của hình nón cần tìm là: \({S_{xq}} = \pi Rl = \pi .\dfrac{{a\sqrt 3 }}{3}.\dfrac{{a\sqrt {21} }}{6} = \dfrac{{\pi {a^2}\sqrt 7 }}{6}\).

Chọn B.