Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

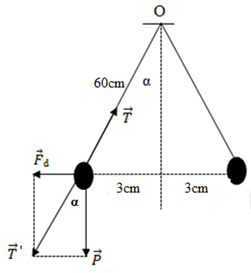
Từ hình vẽ ta có:

\(\tan \alpha  = \dfrac{{{F_d}}}{P} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }} \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.P\)

\( \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.0,5.10 = 0,25N\)

Lại có: \({F_d} = \dfrac{{k{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{{F_d}.{r^2}}}{k}}  = \sqrt {\dfrac{{0,25.{{\left( {{{6.10}^{ - 2}}} \right)}^2}}}{{{{9.10}^9}}}}  = 3,{2.10^{ - 7}}C\)

Chọn D.