Câu hỏi
Cho hình chóp \(SABC\) có đáy là tam giác \(ABC\) vuông cân tại \(A,\)\(SA\) vuông góc với mặt phẳng đáy, \(SA = \dfrac{{a\sqrt 6 }}{2},\,\,AB = a.\) Gọi \(M\) là trung điểm của \(BC.\) Góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABC} \right)\) có số đo bằng:
- A \({45^0}\)
- B \({30^0}\)
- C \({60^0}\)
- D \({90^0}\)
Phương pháp giải:
Góc giữa \(SM\) và \(\left( {ABC} \right)\) là góc giữa \(SM\) và hình chiếu của \(SM\) trên \(\left( {ABC} \right).\)
Lời giải chi tiết:
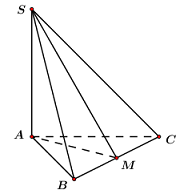
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow AM\) là hình chiếu của \(SM\) trên \(\left( {ABC} \right).\)
\( \Rightarrow \angle \left( {SM,\,\,\left( {ABC} \right)} \right) = \angle \left( {SM,\,\,AM} \right) = \angle SMA.\)
Áp dụng định lý Pi-ta-go cho \(\Delta ABC\) vuông cân tại \(A\) có \(AB = a\) ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\(AM\) là đường trung tuyến của \(\Delta ABC\) \( \Rightarrow AM = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 2 }}{2}.\)
Xét \(\Delta SAM\) vuông tại \(A\) ta có: \(\tan \angle SMA = \dfrac{{SA}}{{AM}} = \dfrac{{a\sqrt 6 }}{2}:\dfrac{{a\sqrt 2 }}{2} = \sqrt 3 \) \( \Rightarrow \angle SMA = {60^0}.\)
Chọn C.







