Phương pháp giải:

- Tính độ dài \(HD\).

- Xác định góc giữa \(SD\) và mặt đáy là góc giữa \(SD\) và hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\).

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường cao \(SH\).

- Sử dụng công thức tính thể tích khối chóp: \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\).

Lời giải chi tiết:

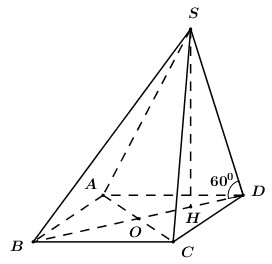
Ta có: \(BD = 1 \Rightarrow HD = \dfrac{1}{4}BD = \dfrac{1}{4}\).

Vì \(SH \bot \left( {ABCD} \right)\) nên \(HD\) là hình chiếu vuông góc của \(SD\) lên \(\left( {ABCD} \right)\).

\( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;HD} \right) = \angle SDH = {60^0}\).

Xét tam giác vuông \(SHD\) có: \(SH = HD.\tan {60^0} = \dfrac{{\sqrt 3 }}{4}\).

Do \(ABCD\) là hình vuông có \(BD = 1 \Rightarrow AB = AD = \dfrac{{BD}}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\) \( \Rightarrow {S_{ABCD}} = AB.AD = \dfrac{1}{{\sqrt 2 }}.\dfrac{1}{{\sqrt 2 }} = \dfrac{1}{2}\).

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 3 }}{4}.\dfrac{1}{2} = \dfrac{{\sqrt 3 }}{{24}}\).

Chọn A.