Phương pháp giải:

Lập tỉ lệ thể tích và đánh giá.

Lời giải chi tiết:

Giả sử \(SA = x\,\,\left( {x > 0} \right)\). Gọi O là tâm của hình vuông \(ABCD\).

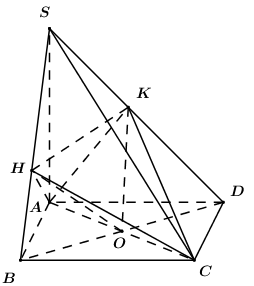
Ta có: \({V_{ACHK}} = {V_{A.OHK}} + {V_{C.OHK}} = 2{V_{A.OHK}}\) (do O là trung điểm AC)

Tam giác SAB vuông tại A, AH là đường cao

\( \Rightarrow SH.SB = S{A^2} \Rightarrow \dfrac{{SH}}{{SB}} = {\left( {\dfrac{{SA}}{{SB}}} \right)^2} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}} \Rightarrow \dfrac{{SH}}{{SB}} = \dfrac{{SK}}{{SD}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}\)

Ta có: \({S_{SHK}} = \dfrac{{SH}}{{SB}}.\dfrac{{SK}}{{SD}}.{S_{SBD}} = {\left( {\dfrac{{{x^2}}}{{{x^2} + {a^2}}}} \right)^2}.{S_{SBD}}\) và

\(\begin{array}{l}{S_{OBH}} = {S_{ODK}} = \dfrac{{BH}}{{SB}}.\dfrac{{BO}}{{BD}}.{S_{SBD}}\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{a^2}}}{{{x^2} + {a^2}}}.\dfrac{1}{2}.{S_{SBD}} = \dfrac{{{a^2}}}{{2\left( {{x^2} + {a^2}} \right)}}.{S_{SBD}}\end{array}\)

\(\begin{array}{l} \Rightarrow {S_{OHK}} = \left( {1 - {{\left( {\dfrac{{{x^2}}}{{{x^2} + {a^2}}}} \right)}^2} - 2.\dfrac{{{a^2}}}{{2\left( {{x^2} + {a^2}} \right)}}} \right){S_{SBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{\left( {{x^2} + {a^2}} \right)}^2} - {x^4} - {a^2}\left( {{x^2} + {a^2}} \right)}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}{S_{SBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{a^2}{x^2}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}{S_{SBD}}\end{array}\)

Ta có:  \(\dfrac{{{V_{A.OHK}}}}{{{V_{A.SBD}}}} = \dfrac{{{S_{OHK}}}}{{{S_{SBD}}}} = \dfrac{{{a^2}{x^2}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}} \Rightarrow \dfrac{{{V_{ACHK}}}}{{{V_{S.ABCD}}}} = \dfrac{{{a^2}{x^2}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}\)\( \Rightarrow {V_{ACHK}} = \dfrac{{{a^2}{x^2}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}{V_{S.ABCD}} = \dfrac{{{a^2}{x^2}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}.\dfrac{1}{3}x{a^2} = \dfrac{{{a^4}}}{3}.\dfrac{{{x^3}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}}\)

Ta có: \(\dfrac{{{x^3}}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}} = \dfrac{{{x^3}}}{{{{\left( {\dfrac{{{x^2}}}{3} + \dfrac{{{x^2}}}{3} + \dfrac{{{x^2}}}{3} + {a^2}} \right)}^2}}} \le \dfrac{{{x^3}}}{{{{\left( {4\sqrt[4]{{\dfrac{{{x^2}}}{3} + \dfrac{{{x^2}}}{3} + \dfrac{{{x^2}}}{3} + {a^2}}}} \right)}^2}}} = \dfrac{{{x^3}}}{{16\sqrt {\dfrac{{{x^6}{a^2}}}{{27}}} }} = \dfrac{{3\sqrt 3 }}{{16a}}\)

\( \Rightarrow {V_{ACHK}} \le \dfrac{{{a^3}\sqrt 3 }}{{16}}\)

Dấu “=” xảy ra khi và chỉ khi \(\dfrac{{{x^2}}}{3} = {a^2} \Leftrightarrow x = a\sqrt 3 \).

Vậy, thể tích khối tứ diện \(ACHK\) lớn nhất bằng \(\dfrac{{{a^3}\sqrt 3 }}{{16}}\) khi \(x = a\sqrt 3 \).

Chọn C.