Câu hỏi
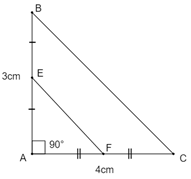
Cho tam giác ABC vuông tại A, \(AB = 3cm\),\(AC = 4cm\). Gọi E là trung điểm của AB, F là trung điểm của AC. Ta tính được độ dài EF là:
- A \(2,5cm\)
- B \(2cm\)
- C \(3cm\)
- D \(5cm\)
Phương pháp giải:
Áp dụng định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Lời giải chi tiết:
Áp dụng định lí Py-ta-go cho \(\Delta ABC\) vuông tại A ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = 5cm\end{array}\)
Mà \(\left\{ \begin{array}{l}AE = EB\,\,\,\left( {gt} \right)\\AF = FC\,\,\,\,\left( {gt} \right)\end{array} \right.\) \( \Rightarrow \)\(EF\) là đường trung bình của \(\Delta ABC\) (định nghĩa)
\( \Rightarrow \)\({\rm{EF}} = \frac{1}{2}BC = \frac{1}{2} \times 5 = 2,5cm\) (tính chất đường trung bình của tam giác).
Chọn A.