Phương pháp giải:

Bước sóng: \(\lambda  = \dfrac{v}{f}\)

Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)

Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:

\( - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }\)

Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với k_max = 6

Sử dụng định lí hàm số cos và các tỉ số lượng giác để tính toán.

Lời giải chi tiết:

Bước sóng: \(\lambda  = \dfrac{v}{f} = \dfrac{{60}}{{40}} = 1,5cm\)

Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:

\(\begin{array}{l} - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda } \Leftrightarrow  - \dfrac{{10}}{{1,5}} < k < \dfrac{{10}}{{1,5}}\\ \Leftrightarrow  - 6,7 < k < 6,7 \Rightarrow k =  - 6; - 5;...;6\end{array}\)

Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với k_max

\({d_2} - {d_1} = {k_{\max }}\lambda  \Leftrightarrow MB - MA = 6.1,5 = 9cm\)

Mà \(MA = AB = 10cm \Rightarrow MB = 19cm\)

Ta có hình vẽ:

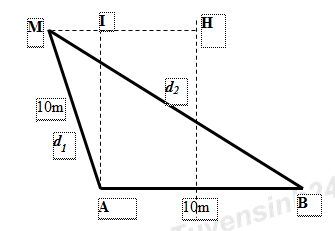
Áp dụng định lí hàm số cos trong tam giác MAB ta có:

\(\begin{array}{l}M{B^2} = M{A^2} + M{B^2} - 2.MA.MB.cos\widehat {MAB} \Rightarrow \widehat {MAB} = 143,{6^0}\\ \Rightarrow \widehat {MAI} = \widehat {MAB} - {90^0} = 53,{6^0}\\ \Rightarrow MI = AB.\sin \widehat {MAI} = 10.0,805 = 8,05cm\\ \Rightarrow b = MH = MI + IH = 8,05 + 5 = 13,05cm\end{array}\)

Chọn B.