Lời giải chi tiết:

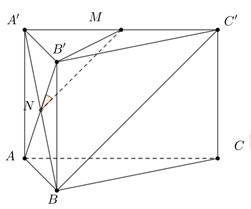
Gọi \(N = AB' \cap A'B\) và \(M\) là trung điểm của \(A'C'\).

Ta có: \(MN\) là đường trung bình của tam giác \(A'C'B\) \( \Rightarrow MN\parallel BC'\) \( \Rightarrow \angle \left( {AB';BC'} \right) = \angle \left( {AB';MN} \right)\).

\( \Rightarrow \angle \left( {AB';MN} \right) = {60^0}\) \( \Rightarrow \angle B'NM = {60^0}\) hoặc \(\angle B'NM = {120^0}\).

Vì \(MN\) là đường trung bình của tam giác \(A'C'B\) nên \(MN = \dfrac{1}{2}BC'\).

Hình chữ nhật \(BCC'B'\) và hình chữ nhật \(ABB'A'\) là hai hình chữ nhật bằng nhau nên \(BC' = AB'\) \( \Rightarrow MN = NB'\).

TH1: \(\angle B'NM = {60^0}\), khi đó \(\Delta B'MN\) đều.

Tam giác \(A'B'C'\) đều cạnh \(a \Rightarrow B'M = \dfrac{{a\sqrt 3 }}{2}\)\( = B'N = MN\).

\( \Rightarrow AB' = 2B'N = a\sqrt 3 \).

Áp dụng định lí Pytago trong tam giác vuông \(AA'B'\) ta có:

\(AA' = \sqrt {AB{'^2} - A'B{'^2}}  = \sqrt {3{a^2} - {a^2}}  = a\sqrt 2 \).

\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\).

TH2: \(\angle B'NM = {120^0}\).

Tam giác \(A'B'C'\) đều cạnh \(a \Rightarrow B'M = \dfrac{{a\sqrt 3 }}{2}\).

Áp dụng định lí Cosin trong tam giác \(B'MN\) ta có:

\(\begin{array}{l}\cos {120^0} = \dfrac{{B'{N^2} + M{N^2} - B'{M^2}}}{{2B'N.MN}}\\ \Leftrightarrow  - \dfrac{1}{2} = \dfrac{{2M{N^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2M{N^2}}}\\ \Leftrightarrow  - M{N^2} = 2M{N^2} - \dfrac{{3{a^2}}}{4}\\ \Leftrightarrow 3M{N^2} = \dfrac{{3{a^2}}}{4}\\ \Leftrightarrow MN = \dfrac{a}{2} = B'N\end{array}\)

\( \Rightarrow AB' = 2B'N = a = AB\) (Vô lí do cạnh huyền không thể bằng cạnh góc vuông).

Vậy \({V_{ABC.A'B'C'}} = \dfrac{{{a^3}\sqrt 6 }}{4}\).

Chọn C.