Phương pháp giải:

- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia. Chứng minh \(d\left( {SB;MN} \right) = d\left( {A;\left( {MNP} \right)} \right)\) với P là trung điểm của SA.

- Xác định khoảng cách bằng phương pháp 3 nét: Kẻ \(AH \bot MN,\,\,AK \bot PH\) và chứng minh \(AK = d\left( {A;\left( {MNP} \right)} \right)\).

- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

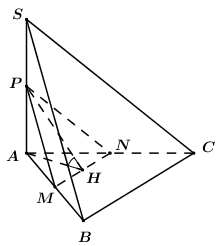
Gọi P là trung điểm của SA.

Ta có: \(MP\parallel SB \Rightarrow SB\parallel \left( {MNP} \right) \supset MN\).

\( \Rightarrow d\left( {SB;MN} \right) = d\left( {SB;\left( {MNP} \right)} \right) = d\left( {B;\left( {MNP} \right)} \right)\).

Lại có: \(AB \cap \left( {MNP} \right) = M \Rightarrow \dfrac{{d\left( {B;\left( {MNP} \right)} \right)}}{{d\left( {A;\left( {MNP} \right)} \right)}} = \dfrac{{BM}}{{AM}} = 1\) \( \Rightarrow d\left( {B;\left( {MNP} \right)} \right) = d\left( {A;\left( {MNP} \right)} \right)\).

Trong (ABC), dựng \(AH \bot MN\,\,\left( {H \in MN} \right)\), trong (APH) dựng \(AK \bot PH\,\,\left( {K \in PH} \right)\) ta có:

 \(\begin{array}{l}\left\{ \begin{array}{l}MN \bot AH\\MN \bot PA\end{array} \right. \Rightarrow MN \bot \left( {APH} \right) \Rightarrow MN \bot AK\\\left\{ \begin{array}{l}AK \bot PH\\AK \bot MN\end{array} \right. \Rightarrow AK \bot \left( {MNP} \right)\\ \Rightarrow d\left( {A;\left( {MNP} \right)} \right) = AK \Rightarrow d\left( {SB;MN} \right) = AK\end{array}\)

Do \(\left( {MNP} \right)\parallel \left( {SBC} \right)\), mà theo giả thiết ta có \(\angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = {60^0}\) \( \Rightarrow \angle \left( {\left( {MNP} \right);\left( {ABC} \right)} \right) = {60^0}\).

Ta có: \(\left\{ \begin{array}{l}\left( {MNP} \right) \cap \left( {ABC} \right) = MN\\AH \subset \left( {ABC} \right),\,\,AH \bot MN\\PH \subset \left( {MNP} \right),\,\,PH \bot MN\,\,\left( {do\,\,MN \bot \left( {APH} \right)} \right)\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {MNP} \right);\left( {ABC} \right)} \right) = \angle \left( {AH;PH} \right) = \angle AHP = {60^0}\).

Tam giác ABC đều cạnh a suy ra tam giác \(AMN\) đều cạnh \(\dfrac{a}{2}\)\( \Rightarrow AH = \dfrac{{\dfrac{a}{2}.\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}.\)

Tam giác AHK vuông tại K \( \Rightarrow AK = AH.\sin \angle AHP = \dfrac{{a\sqrt 3 }}{4}.\sin {60^0} = \dfrac{{3a}}{8}\).

Vậy \(d\left( {SB;MN} \right) = AK = \dfrac{{3a}}{8}\).

Chọn D.