Câu hỏi
Khẳng định nào sau đây là đúng?
- A \(y = \left| {\tan x} \right|\) đồng biến trong \(\left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]\).
- B \(y = \left| {\tan x} \right|\) là hàm số chẵn trên \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
- C \(y = \left| {\tan x} \right|\) có đồ thị đối xứng qua gốc tọa độ.
- D \(y = \left| {\tan x} \right|\) luôn nghịch biến trong \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\).
Phương pháp giải:
- Từ đồ thị hàm số \(y = \tan x\) vẽ đồ thị hàm số \(y = \left| {\tan x} \right|\) bằng cách giữa lại phần đồ thị nằm phía trên trục Ox, lấy đối xứng phần đồ thị phía dưới trục Ox qua trục Ox sau đó xóa đi phần đồ thị phía dưới trục Ox.
- Dựa vào đồ thị hàm số \(y = \left| {\tan x} \right|\) vẽ được để chọn đáp án đúng.
Lời giải chi tiết:
Ta có đồ thị hàm số \(y = \left| {\tan x} \right|\) như sau:
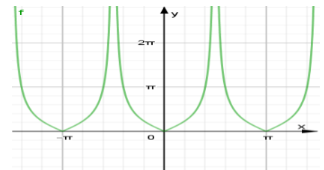
TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Dựa vào đồ thị hàm số ta thấy:
- Hàm số \(y = \left| {\tan x} \right|\) nghịch biến trên \(\left( { - \dfrac{\pi }{2};0} \right)\) và đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\), do đó đáp án A và D sai.
- Đặt \(f\left( x \right) = \left| {\tan x} \right|\), \(\forall x \in D \Rightarrow - x \in D\).
\(f\left( { - x} \right) = \left| {\tan \left( { - x} \right)} \right| = \left| { - \tan x} \right| = \left| {\tan x} \right| = f\left( x \right)\), do đó hàm số đã cho là hàm chẵn trên tập xác định. Do đó đáp án B đúng.
- Do là hàm chẵn nên đồ thị hàm số đối xứng qua trục Oy chứ không đố![]() i xứng qua tâm O, do đó đáp án C sai.
i xứng qua tâm O, do đó đáp án C sai.
Chọn B.







