Phương pháp giải:

- Chứng minh \(SM \bot \left( {ABCD} \right)\).

- Trong (ABCD) kẻ \(MI \bot ND\,\,\left( {I \in ND} \right)\), trong (SMI) kẻ \(MH \bot SI\). Chứng minh \(MH = d\left( {M;\left( {SND} \right)} \right)\).

- Tính \({S_{MND}}\), từ đó tính MI.

- Áp dụng hệ thức lượng trong tam giác vuông tính SM, từ đó suy ra \(d\left( {G;\left( {ABCD} \right)} \right)\).

- Tính diện tích tứ giác AMND: \({S_{AMND}} = {S_{ABCD}} - {S_{BMN}} - {S_{CND}}\).

- Áp dụng công thức tính thể tích: \({V_{G.AMND}} = \dfrac{1}{3}d\left( {G;\left( {ABCD} \right)} \right).{S_{AMND}}\).

Lời giải chi tiết:

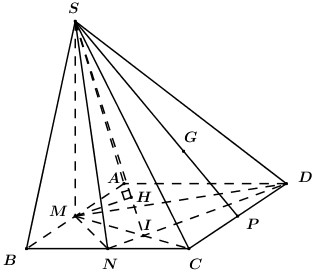
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right) = AB\\SM \subset \left( {SAB} \right),\,\,SM \bot AB\end{array} \right.\)\( \Rightarrow SM \bot \left( {ABCD} \right)\).

Trong (ABCD) kẻ \(MI \bot ND\,\,\left( {I \in ND} \right)\), trong (SMI) kẻ \(MH \bot SI\).

Ta có: \(\left\{ \begin{array}{l}ND \bot MI\\ND \bot SM\end{array} \right. \Rightarrow ND \bot \left( {SMI} \right) \Rightarrow ND \bot MH\).

            \(\left\{ \begin{array}{l}MH \bot ND\\MH \bot SI\end{array} \right. \Rightarrow MH \bot \left( {SND} \right)\) \( \Rightarrow d\left( {M;\left( {SND} \right)} \right) = MH = \dfrac{{3a\sqrt 2 }}{4}\).

Ta có:

\(\begin{array}{l}{S_{BMN}} = \dfrac{1}{2}BM.BN = \dfrac{1}{2}.a.a = \dfrac{{{a^2}}}{2}\\{S_{AMD}} = \dfrac{1}{2}AM.AD = \dfrac{1}{2}.a.2a = {a^2}\\{S_{CND}} = \dfrac{1}{2}CN.CD = \dfrac{1}{2}.a.2a = {a^2}\\{S_{ABCD}} = A{B^2} = 4{a^2}\\ \Rightarrow {S_{MND}} = {S_{ABCD}} - {S_{BMN}} - {S_{AMD}} - {S_{CND}}\\ \Rightarrow {S_{MND}} = 4{a^2} - \dfrac{{{a^2}}}{2} - {a^2} - {a^2} = \dfrac{{3{a^2}}}{2}\end{array}\)

Lại có \(ND = \sqrt {C{N^2} + C{D^2}}  = \sqrt {{a^2} + 4{a^2}}  = a\sqrt 5 \), \({S_{MND}} = \dfrac{1}{2}MI.ND\).

\( \Rightarrow MI = \dfrac{{2{S_{MND}}}}{{ND}} = \dfrac{{2.\dfrac{{3{a^2}}}{2}}}{{a\sqrt 5 }} = \dfrac{{3a\sqrt 5 }}{5}\).

Áp dụng hệ thức lượng trong tam giác vuông SMI có:

\(\begin{array}{l}\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{N^2}}}\\\dfrac{1}{{{{\left( {\dfrac{{3a\sqrt 2 }}{4}} \right)}^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{{{\left( {\dfrac{{3a\sqrt 5 }}{5}} \right)}^2}}}\\ \Rightarrow \dfrac{1}{{S{M^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SM = a\sqrt 3 \end{array}\)

Gọi P là trung điểm của CD, ta có \(SG \cap \left( {ABCD} \right) = P\) \( \Rightarrow \dfrac{{d\left( {G;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \dfrac{{GP}}{{SP}} = \dfrac{1}{3}\)

\( \Rightarrow d\left( {G;\left( {ABCD} \right)} \right) = \dfrac{1}{3}SM = \dfrac{{a\sqrt 3 }}{3}\).

\(\begin{array}{l}{S_{AMND}} = {S_{ABCD}} - {S_{BMN}} - {S_{CND}}\\{S_{AMND}} = 4{a^2} - \dfrac{1}{2}{a^2} - {a^2} = \dfrac{{5{a^2}}}{2}\end{array}\)

Vậy \({V_{G.AMND}} = \dfrac{1}{3}d\left( {G;\left( {ABCD} \right)} \right).{S_{AMND}}\) \( = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{{5{a^2}}}{2} = \dfrac{{5\sqrt 3 {a^3}}}{{18}}\).

Chọn D.