Câu hỏi
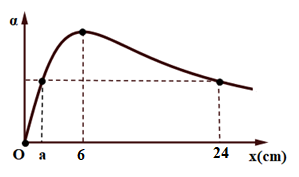
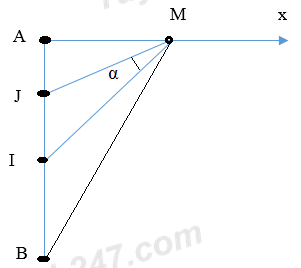
Hai nguồn sáng đồng bộ A, B dao động trên mặt nước, I là trung điểm của AB, điểm J trên đoạn IA và IJ = 5 cm. Điểm M trên mặt nước nằm trên đường thẳng vuông góc với AB và đi qua A, với AM = x. Đồ thị hình bên biểu diễn sự phụ thuộc của góc \(\alpha = \angle {\rm{IMJ}}\) vào x. Khi x = b cm và x = 24 cm thì M tương tương ứng là điểm dao động cực đại gần và xa A nhất. Tỉ số \(\frac{b}{a}\) gần với giá trị nào nhất sau đây?
- A 4,92
- B 5,25
- C 5,05
- D 4,70
Phương pháp giải:
Vẽ hình theo các dữ kiện của bài.
Áp dụng biểu thức:
\(\tan \left( {{\varphi _1} - {\varphi _2}} \right) = \frac{{\tan {\varphi _1} - \tan {\varphi _2}}}{{1 + \tan {\varphi _1}.\tan {\varphi _2}}}\)
Điều kiện có cực đại giao thoa:
\({d_2} - {d_1} = k\lambda ;\,k \in Z\)
Ta tìm được số cực đại trên AB là số giá trị k thỏa mãn
\(\frac{{ - AB}}{\lambda } < k < \frac{{AB}}{\lambda }\)
Tìm được k, ta xác định vị trí M (b) là điểm cực đại gần A nhất thỏa mãn:
\(BM' - AM' = k\lambda \)
Lời giải chi tiết:
Ta có hình vẽ
Áp dụng biểu thức:
\(\begin{array}{l}
\tan \alpha = \tan \left( {\angle {\rm{IMJ}}} \right) = \tan \left( {\angle IMA - \angle JMA} \right)\\
\Leftrightarrow \tan \alpha = \frac{{\tan \left( {\angle IMA} \right) - \tan \left( {\angle JMA} \right)}}{{1 + \tan \left( {\angle IMA} \right).\tan \left( {\angle JMA} \right)}}\\
\Leftrightarrow \tan \alpha = \frac{{\frac{{AI}}{{AM}} - \frac{{{\rm{AJ}}}}{{AM}}}}{{1 + \frac{{AI}}{{AM}}.\frac{{{\rm{AJ}}}}{{AM}}}} = \frac{{\frac{{{\rm{IJ}}}}{{AM}}}}{{1 + \frac{{AI.{\rm{AJ}}}}{{A{M^2}}}}} = \frac{{{\rm{IJ}}}}{{AM + \frac{{AI.{\rm{AJ}}}}{{AM}}}} = \frac{5}{{x + \frac{{AI.{\rm{AJ}}}}{x}}}
\end{array}\)
Biết rằng hàm tanα là hàm đồng biến, nên khi α cực đại thì tanα cực đại.
\({(\tan \alpha )_{\max }} \Leftrightarrow {\left( {x + \frac{{AI.{\rm{AJ}}}}{x}} \right)_{\min }}\)
Áp dụng BĐT Cosi ta có:
\(\begin{array}{l}
x + \frac{{AI.{\rm{AJ}}}}{x} \ge 2\sqrt {AI.{\rm{AJ}}} \\
\Rightarrow \left( {x + \frac{{AI.{\rm{AJ}}}}{x}} \right)\min \Leftrightarrow x = \frac{{AI.{\rm{AJ}}}}{x} \Leftrightarrow {x^2} = AI.{\rm{AJ}}
\end{array}\)
Từ đồ thị khi x = 6 thì α cực đại, nên:
\(AI.AJ = {6^2} = 36\)
Tại x = 24 và x = a thì có cùng giá trị góc α. Ta có
\(\begin{array}{l}
\tan \alpha = \frac{5}{{24 + \frac{{36}}{{24}}}} = \frac{5}{{a + \frac{{36}}{a}}} \Rightarrow a + \frac{{36}}{a} = 25,5\\
\Leftrightarrow {a^2} - 25,5a + 36 = 0 \Leftrightarrow \left[ \begin{array}{l}
{a_1} = 1,5cm\\
{a_2} = 24cm
\end{array} \right.
\end{array}\)
Vậy a = 1,5cm.
Từ AI.AJ = 36, mà IJ = 5 cm, nên ta có:
\(\left\{ \begin{array}{l}
AI.{\rm{AJ}} = 36\\
AI = AJ + 5
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
AI = 9cm\\
AJ = 4cm
\end{array} \right.\)
Vậy AB = 2AI = 18 cm.
Khi M ở vị trí x = 24 cm thì M là cực đại xa A nhất, áp dụng điều kiện cực đại cho M ta có
\(\begin{array}{l}
BM - AM = \lambda \Leftrightarrow \sqrt {B{A^2} + A{M^2}} - AM = \lambda \\
\Rightarrow \lambda = \sqrt {{{18}^2} + {{24}^2}} - 24 = 6cm
\end{array}\)
Số cực đại trên AB thỏa mãn điều kiện:
\(\frac{{ - AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow \frac{{ - 18}}{6} < k < \frac{{18}}{6} \Rightarrow - 3 < k < 3\)
Không kể hai nguồn A, B, khi M ở vị trí x = b thì M là cực đại gần A nhất, ứng với k = 2, ta có:
\(\begin{array}{l}
BM' - AM' = 2\lambda \Leftrightarrow \sqrt {B{A^2} + AM{'^2}} - AM' = 2\lambda \\
\Rightarrow \lambda = \sqrt {{{18}^2} + {b^2}} - b = 2.6 = 12 \Rightarrow b = 7,5cm
\end{array}\)
Ta có tỉ số
\(\frac{b}{a} = \frac{{7,5}}{{1,5}} = 5\)
Vậy giá trị gần nhất là 5,05.
Chọn C.







