Câu hỏi
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây
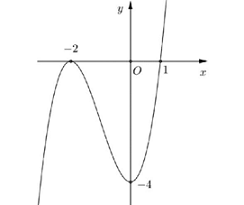
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\)nghiệm phân biệt
- A \(2\).
- B \(4\).
- C \(3\).
- D \(5\).
Phương pháp giải:
Đặt ẩn phụ \(t = \left| {f\left( x \right)} \right|\) để đưa về phương trình bậc hai.
Áp dụng định lý Viét để tìm nghiệm của phương trình.
Cô lập tham số m theo t rồi biện luận.
Lời giải chi tiết:
Ta có \({f^2}\left( x \right) - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0 \Leftrightarrow {\left| {f\left( x \right)} \right|^2} - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0\)
Đặt \(t = \left| {f\left( x \right)} \right|\). Khi đó ta có phương trình:
\({t^2} - \left( {m + 4} \right)t + 2m + 4 = 0 \Rightarrow \left\{ \begin{array}{l}{t_1} + {t_2} = m + 4\\{t_1}{t_2} = 2m + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 2\\{t_2} = m + 2\end{array} \right.\)
+) \({t_1} = 2 \Rightarrow \left| {f\left( x \right)} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 2\\f\left( x \right) = - 2\end{array} \right. \Rightarrow \) tổng có 4 nghiệm \(\left\{ \begin{array}{l}{x_1} \in \left( {1; + \infty } \right)\\{x_2} \in \left( {0;1} \right)\\{x_3} \in \left( { - 2;0} \right)\\{x_4} \in \left( { - \infty ; - 2} \right)\end{array} \right.\)
+)\({t_2} = m + 2 \Leftrightarrow \left| {f\left( x \right)} \right| = m + 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = m + 2 \in \left( { - 3;7} \right)\\f\left( x \right) = - m - 2 \in \left( { - 7;3} \right)\end{array} \right.\) có hai nghiệm phân biệt khác các nghiệm trên.
+) \(m + 2 = - m - 2 = 0 \Leftrightarrow m = - 2 \Rightarrow \) phương trình có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = - 2\\{x_2} = 1\end{array} \right.\left( {tm} \right)\)
+) \(\left\{ \begin{array}{l}m + 2 > 0;m + 2 \ne 2\\ - m - 2 < - 4; - m - 2 \ne - 2\end{array} \right. \Leftrightarrow 2 < m < 5 \Rightarrow \) có 2 số thỏa mãn.
+) \(\left\{ \begin{array}{l}m + 2 > 0;m + 2 \ne 2\\ - m - 2 > 0; - m - 2 \ne 2\\m \ne - 2\end{array} \right. \Rightarrow \) không có m thỏa mãn.
Vậy có tất cả 3 số nguyên m thỏa mãn.
Chọn C.







