Câu hỏi
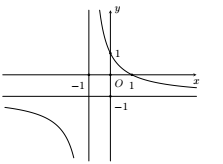
Hàm số nào sau đây có đồ thị như hình vẽ bên ?
- A \(y = \dfrac{{ - x}}{{x + 1}}\).
- B \(y = \dfrac{{ - 2x + 1}}{{2x + 1}}\).
- C \(y = \dfrac{{ - x + 2}}{{x + 1}}\).
- D \(y = \dfrac{{ - x + 1}}{{x + 1}}\).
Phương pháp giải:
- Dựa vào đồ thị suy ra tiệm cận ngang; tiệm cận đứng của hàm số.
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TCN: \(y = \dfrac{a}{c}\) và TCĐ \(x = - \dfrac{d}{c}\).
- Dựa vào các đường tiệm cận và các điểm đi qua để tìm các hệ số.
Lời giải chi tiết:
Gọi phương trình hàm số dạng \(y = \dfrac{{ax + b}}{{cx + d}}\).
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có đường tiệm cận ngang \(y = - 1;\) và tiệm cận đứng là \(x = - 1\).
Khi đó ta có: \(\left\{ \begin{array}{l}\dfrac{a}{c} = - 1\\ - \dfrac{d}{c} = - 1\end{array} \right.\). Chọn \(c = 1 \Rightarrow \left\{ \begin{array}{l}a = - 1\\d = 1\end{array} \right.\)
Khi đó hàm số có dạng \(y = \dfrac{{ - x + b}}{{x + 1}}\).
Lại có đồ thị hàm số đi qua điểm có tọa độ \(\left( {0;1} \right)\) nên ta có: \(1 = \dfrac{{ - 0 + b}}{{0 + 1}} \Leftrightarrow b = 1\).
Vậy hàm số cần tìm là: \(y = \dfrac{{ - x + 1}}{{x + 1}}\).
Chọn D.







