Câu hỏi
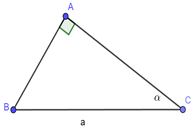
Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\)
Câu 1:
Lập công thức để tính diện tích tam giác ABC theo \(a\) và .
- A \(\frac{1}{2}{a^2}\sin \alpha .\cos \alpha \)
- B \({a^2}\sin \alpha .\cos \alpha \)
- C \(2{a^2}\sin \alpha .\cos \alpha \)
- D \(3{a^2}\sin \alpha .\cos \alpha \)
Phương pháp giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \frac{1}{2}AB.AC.\)
Lời giải chi tiết:
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}AB = BC.\sin \alpha = a.\sin \alpha \\AC = BC.cos\alpha = a.cos\alpha \end{array} \right.\)
\({S_{ABC}} = \frac{1}{2}.AB.AC = \frac{1}{2}a.\sin \alpha .a.cos\alpha = \frac{1}{2}{a^2}.\sin \alpha .cos\alpha \)
Chọn A.
Câu 2:
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy và vẽ hình minh họa.
- A \(\alpha = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \frac{1}{2}{a^2}\)
- B \(\alpha = {30^0}\,\,;\,\,\max {S_{\Delta ABC}} = \frac{{\sqrt 3 }}{4}{a^2}\)
- C \(\alpha = {60^0}\,\,;\,\,\max {S_{\Delta ABC}} = \frac{{\sqrt 3 }}{4}{a^2}\)
- D \(\alpha = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \frac{1}{4}{a^2}\)
Phương pháp giải:
Sử dụng định lý Pitago.
Áp dụng bất đẳng thức Cô-si
Lời giải chi tiết:
\({S_{ABC}} = \frac{1}{2}.AB.AC \le \frac{1}{2}.\frac{{\left( {A{B^2} + A{C^2}} \right)}}{2} = \frac{1}{4}.\left( {A{B^2} + A{C^2}} \right)\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Rightarrow {S_{ABC}} = \frac{1}{2}.AB.AC \le \frac{1}{4}.\left( {A{B^2} + A{C^2}} \right) = \frac{1}{4}B{C^2} = \frac{1}{4}{a^2}\)
Dấu “=” xảy ra \( \Leftrightarrow AC = AB\)\( \Leftrightarrow \Delta ABC\) vuông cân \( \Rightarrow \angle B = \angle C = {45^0}\) hay \(\alpha = {45^0}\).
Vậy \({S_{ABCmax}} = \frac{1}{4}{a^2}\) khi \(\alpha = {45^0}.\)
Chọn D.