Câu hỏi
Cho tam giác \(ABC\) vuông tại \(A\). Kẻ đường cao \(AH.\) Tính \(\sin B;\,\,\sin C\) trong mỗi trường hợp sau:
Câu 1:
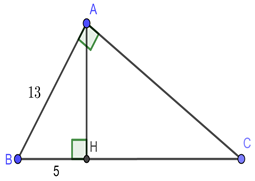
Biết \(AB{\rm{ }} = {\rm{ 13}}cm,BH = 5cm\).
- A \(\sin B = \frac{5}{{13}}\,\,;\,\,\sin C = \frac{{12}}{{13}}\)
- B \(\sin B = \frac{8}{{13}}\,\,;\,\,\sin C = \frac{5}{{13}}\)
- C \(\sin B = \frac{{12}}{{13}}\,\,;\,\,\sin C = \frac{5}{{13}}\)
- D \(\sin B = \frac{5}{{13}}\,\,;\,\,\sin C = \frac{8}{{13}}\)
Phương pháp giải:
Áp dụng định lý Pitago để tính độ dài cạnh AH.
Áp dụng hệ thức về cạnh và góc trong tam giác vuông: \(\sin B = \frac{{AH}}{{AB}}.\)
Áp dụng hệ thức lượng trong tam giác vuông để tính cạnh BC.
Từ đó tính: \(\sin C = \frac{{AB}}{{BC}}.\)
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) có:
\(A{H^2} + B{H^2} = A{B^2}\) \( \Leftrightarrow A{H^2} + {5^2} = {13^2}\)
\( \Leftrightarrow A{H^2} = 144 \Rightarrow AH = 12\,cm.\)
Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(\sin B = \frac{{AH}}{{AB}} = \frac{{12}}{{13}}\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có: \(A{B^2} = BH.BC\) \( \Leftrightarrow {13^2} = 5.BC \Rightarrow BC = \frac{{169}}{5}\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin C = \frac{{AB}}{{BC}} = 13:\frac{{169}}{5} = \frac{5}{{13}}\)
Chọn C.
Câu 2:
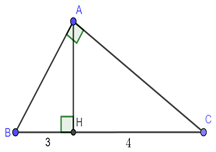
Biết \(BH{\rm{ }} = {\rm{ 3}}cm,CH = 4cm\)
- A \(\sin B = \frac{{\sqrt 7 }}{7}\,\,;\,\,\,\sin C = \frac{{\sqrt {21} }}{7}\)
- B \(\sin B = \frac{{2\sqrt 7 }}{7}\,\,;\,\,\,\sin C = \frac{{\sqrt {21} }}{7}\)
- C \(\sin B = \frac{{\sqrt 7 }}{7}\,\,;\,\,\,\sin C = \frac{{3\sqrt 7 }}{7}\)
- D \(\sin B = \frac{{2\sqrt 7 }}{7}\,\,;\,\,\,\sin C = \frac{{3\sqrt 7 }}{7}\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông \(A{B^2} = BH.BC\); \(A{C^2} = CH.BC\)
Sử dụng hệ thức về cạnh và góc để tính \(\sin B,\,\,\sin C.\)
Lời giải chi tiết:
Ta có: \(BC = BH + CH = 3 + 4 = 7cm.\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\) \( \Leftrightarrow A{B^2} = 3.7\)\( \Rightarrow AB = \sqrt {21} \)
\(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 4.7\)\( \Rightarrow AC = \sqrt {28} \)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}\sin B = \frac{{AC}}{{BC}} = \frac{{\sqrt {28} }}{7} = \frac{{2\sqrt 7 }}{7}\\\sin C = \frac{{AB}}{{BC}} = \frac{{\sqrt {21} }}{7} = \frac{{\sqrt {21} }}{7}\end{array} \right.\)
Chọn B.