Câu hỏi
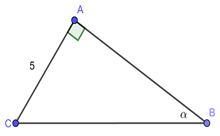
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC{\rm{ }} = {\rm{ 5}}cm,\angle B = \alpha ,\) biết \({\rm{cot}}B = 2,4.\) Tính \(AB,\,\,BC.\)
- A \(AB = 10cm\,\,\,;\,\,\,BC = 12cm\)
- B \(AB = 6cm\,\,\,;\,\,\,BC = 8cm\)
- C \(AB = 7cm\,\,\,;\,\,\,BC = 12cm\)
- D \(AB = 12cm\,\,\,;\,\,\,BC = 13cm\)
Phương pháp giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông \(AB = AC\cot B.\)
Sử dụng định lý Pitago để tính độ dài cạnh BC.
Lời giải chi tiết:
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = AC.cotB = 5.2,4 = 12\,\,cm.\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {5^2} + {12^2} = 169\)\( \Rightarrow BC = 13\,\,cm\)
Chọn D.
Câu hỏi trước
