Phương pháp giải:

Gọi biên độ bụng là 2a, thì biên độ của M là  

\({A_M} = \left| {2a.\sin \left( {2\pi .\frac{d}{\lambda }} \right)} \right|\)

Vận tốc cực đại của phần tử M và N là:  

\(\left\{ \begin{array}{l}
{v_{M\max }} = \omega {A_M}\\
{v_{B\max }} = \omega .{A_B}
\end{array} \right.\)

Áp dụng giản đồ vecto quay tìm thời gian mà vận tốc của phần tử B nhỏ hơn vận tốc cực đại của phần tử M.

Áp dụng công thức tính vận tốc sóng  \(v = \frac{\lambda }{T}\)

Lời giải chi tiết:

Bước sóng : \(\lambda = 4AB = 4.18 = 72cm\)

Biên độ của M là:  

\({A_M} = \left| {2a.\sin \left( {2\pi .\frac{{12}}{{72}}} \right)} \right| = a\sqrt 3 \)

Vận tốc cực đại của phần tử M và N là  

\(\left\{ \begin{array}{l}
{v_{M\max }} = \omega a\sqrt 3\
{v_{B\max }} = \omega .2a
\end{array} \right.\)

Áp dụng giản đồ vecto quay:

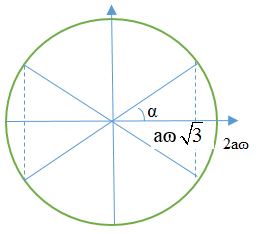
Ta có  

\(\alpha = {\rm{ar}}\cos \frac{{a\sqrt 3 \omega }}{{2a\omega }} = \frac{\pi }{6}\)

Thời gian trong 1 chu kì mà tốc độ dao động của phần tử B không lớn hơn vận tốc cực đại của phần tử M là

\(\Delta t = \frac{T}{{2\pi }}.4\left( {\frac{\pi }{2} - \alpha } \right) = \frac{T}{{2\pi }}.4\left( {\frac{\pi }{2} - \frac{\pi }{6}} \right) = \frac{{2T}}{3} = 0,1s \Rightarrow T = 0,15s\)

Tốc độ truyền sóng trên dây là :

\(v = \frac{\lambda }{T} = \frac{{72}}{{0,15}} = {480_{}}\left( {cm/s} \right) = 4,{8_{}}\left( {m/s} \right)\)

Chọn C.