 Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
Câu hỏi
Dao động của một vật có khối lượng \(200g\) là tổng hợp của hai dao động điều hòa thành phần cùng tần số, cùng biên độ có li độ phụ thuộc thời gian được biểu diễn như hình vẽ. Biết \({t_2} - {t_1} = \dfrac{1}{3}s\). Lấy \({\pi ^2} = 10\). Mốc thế năng ở vị trí cân bằng. Cơ năng của chất điểm có giá trị là:
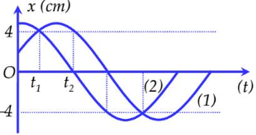
- A \(\dfrac{{6,4}}{3}mJ\)
- B \(\dfrac{{0,64}}{3}mJ\)
- C \(64J\)
- D \(6,4mJ\)
Phương pháp giải:
+ Đọc đồ thị dao động
+ Sử dụng vòng tròn lượng giác
+ Sử dụng công thức góc quét: \(\Delta \varphi = \omega \Delta t\)
+ Sử dụng biểu thức tổng hợp dao động điều hòa: \(x = {x_1} + {x_2} = {A_1}\angle {\varphi _1} + {A_2}\angle {\varphi _2}\)
+ Sử dụng biểu thức tính cơ năng: \({\rm{W}} = \dfrac{1}{2}m{\omega ^2}{A^2}\)
Lời giải chi tiết:
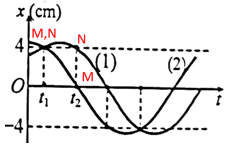
Xét điểm M (đường 2), N (đường 1) tại hai thời điểm \({t_1},{t_2}\) trên đồ thị
Xác định trên vòng tròn lượng giác ta được:
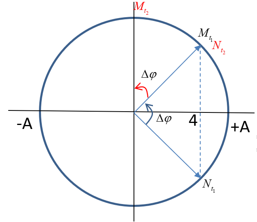
Từ vòng tròn lượng giác, ta suy ra \(\Delta \varphi = \dfrac{\pi }{3}\)
Ta có:
\(\begin{array}{l}{x_{{N_{{t_1}}}}} = 4 = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{6}\\ \Rightarrow A = \dfrac{8}{{\sqrt 3 }}cm\end{array}\)
Mặt khác: \(\Delta \varphi = \omega .\Delta t \Rightarrow \omega = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{\pi }{3}}}{{\dfrac{1}{3}}} = \pi \left( {rad/s} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}{x_1} = \dfrac{8}{{\sqrt 3 }}cos\left( {\pi t - \dfrac{\pi }{6}} \right)cm\\{x_2} = \dfrac{8}{{\sqrt 3 }}cos\left( {\pi t + \dfrac{\pi }{6}} \right)cm\end{array} \right.\)
Dao động tổng hợp: \(x = {x_1} + {x_2} = \dfrac{8}{{\sqrt 3 }}\angle - \dfrac{\pi }{6} + \dfrac{8}{{\sqrt 3 }}\angle \dfrac{\pi }{6} = 8\angle 0\)
Cơ năng của chất điểm: \({\rm{W}} = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}.0,2.{\pi ^2}.{\left( {0,08} \right)^2} = 6,{4.10^{ - 3}}J = 6,4mJ\)
Chọn D






