Phương pháp giải:

- Dựng \(AM \bot SB\), chứng minh \(CM \bot SB\) và xác định góc giữa (SAB) và (SBC) là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính AM, CM, sử dụng định lí Cosin trong tam giác.

- Đặt \(SH = x\), tính SA, SB theo x.

- Áp dụng định lí Cosin trong tam giác SAB tìm x theo a.

- Tính thể tích khối chóp \(V = \dfrac{1}{3}SH.{S_{\Delta ABC}}\).

Lời giải chi tiết:

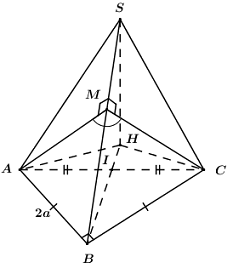
Tam giác ABC vuông cân tại B nên BI là đường trung trực của AC.

Có \(H \in BI\) nên \(HA = HC\).

Xét \(\Delta SHA\) và \(\Delta SHC\) có: \(\angle SHA = \angle SHC = {90^0}\), SH chung, HA = HC.

\( \Rightarrow \Delta SHA = \Delta SHC\) (2 cạnh góc vuông) \( \Rightarrow SA = SC\).

\( \Rightarrow \Delta SAB = \Delta SCB\,\,\left( {c.c.c} \right)\).

Trong (SAB) kẻ \(AM \bot SB\). Suy ra \(CM \bot SB\) (hai chiều cao tương ứng của 2 tam giác bằng nhau).

Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\AM \subset \left( {SAB} \right),\,\,AM \bot SB\\CM \subset \left( {SBC} \right),\,\,CM \bot SB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SBC} \right)} \right) = \angle \left( {AM;CM} \right) = {60^0}\).

Nếu \(\angle AMC = {60^0}\) \( \Rightarrow \Delta ACM\) đều \( \Rightarrow AM = AC > AB\) (mâu thuẫn dó AM là đường vuông góc, AB là đường xiên) \( \Rightarrow \angle AMC = {120^0}\).

Tam giác ABC vuông cân tại B có AB = 2a \( \Rightarrow AC = 2a\sqrt 2 \).

Áp dụng định lí Cosin trong tam giác AMC có:

\(\begin{array}{l}\cos {120^0} = \dfrac{{A{M^2} + M{C^2} - A{C^2}}}{{2.AM.MC}}\\ \Leftrightarrow  - \dfrac{1}{2} = \dfrac{{2A{M^2} - 8{a^2}}}{{2A{M^2}}}\\ \Leftrightarrow  - A{M^2} = 2A{M^2} - 8{a^2}\\ \Leftrightarrow 3A{M^2} = 8{a^2}\\ \Leftrightarrow A{M^2} = \dfrac{{8{a^2}}}{3} \Rightarrow AM = \dfrac{{2a\sqrt 6 }}{3} = CM\end{array}\)

Tam giác ABC vuông cân tại B \( \Rightarrow BI = \dfrac{1}{2}AC = \dfrac{1}{2}.2a\sqrt 2  = a\sqrt 2 \) \( \Rightarrow IH = \dfrac{1}{3}BI = \dfrac{{a\sqrt 2 }}{3}\).

Áp dụng định lí Pytago trong tam giác vuông AHI có: \(AH = \sqrt {A{I^2} + I{H^2}}  = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{3}} \right)}^2}}  = \dfrac{{2a\sqrt 5 }}{3}\).

Đặt \(SH = x\) ta có: \(SA = \sqrt {S{H^2} + A{H^2}}  = \sqrt {{x^2} + \dfrac{{20{a^2}}}{9}} \).

\(BH = BI + IH = a\sqrt 2  + \dfrac{{a\sqrt 2 }}{3} = \dfrac{{4a\sqrt 2 }}{3}\) \( \Rightarrow SB = \sqrt {S{H^2} + B{H^2}}  = \sqrt {{x^2} + \dfrac{{32{a^2}}}{9}} \).

Xét tam giác vuông AMB có: \(\sin \angle ABM = \dfrac{{AM}}{{AB}} = \dfrac{{2a\sqrt 6 }}{3}:2a = \dfrac{{\sqrt 6 }}{3}\) \( \Rightarrow \cos \angle ABM = \dfrac{{\sqrt 3 }}{3}\).

Áp dụng định lí Cosin trong tam giác SAB ta có:

\(\begin{array}{l}\cos \angle ABM = \dfrac{{A{B^2} + S{B^2} - S{A^2}}}{{2AB.SB}}\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{3} = \dfrac{{4{a^2} + {x^2} + \dfrac{{32{a^2}}}{9} - {x^2} - \dfrac{{20{a^2}}}{9}}}{{2.2a.\sqrt {{x^2} + \dfrac{{32{a^2}}}{9}} }}\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{3} = \dfrac{{\dfrac{{16{a^2}}}{3}}}{{2.2a.\sqrt {{x^2} + \dfrac{{32{a^2}}}{9}} }}\\ \Leftrightarrow \sqrt 3  = \dfrac{{4a}}{{\sqrt {{x^2} + \dfrac{{32{a^2}}}{9}} }}\\ \Leftrightarrow 3\left( {{x^2} + \dfrac{{32{a^2}}}{9}} \right) = 16{a^2}\\ \Leftrightarrow 3{x^2} = \dfrac{{16{a^2}}}{3}\\ \Leftrightarrow {x^2} = \dfrac{{16{a^2}}}{9} \Leftrightarrow x = \dfrac{{4a}}{3}\end{array}\)

\( \Rightarrow SH = \dfrac{{4a}}{3}\).

\({S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.{\left( {2a} \right)^2} = 2{a^2}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{2}.\dfrac{{4a}}{3}.2{a^2} = \dfrac{{8{a^3}}}{9}\).

Chọn B.